Сила гидравлического сопротивления

В другом предельном случае (турбулентный режим) - 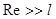- также получена эмпирическая формула для силы сопротивления движению. Она носит название силы гидравлического сопротивления.

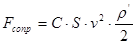. (11)

Здесь 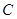- безразмерный коэффициент, зависящий от формы тела;

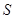- наибольшее сечение тела в плоскости, перпендикулярной потоку, [];

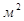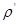- плотность среды, [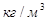];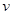- относительная скорость движения тела в среде, [].

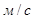Приближенные значения коэффициента 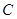для тел различной формы:

Тело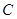
Плоская платина, перпендикулярная потоку	1.11
Открытая полусфера отверстием навстречу потоку	1.33
Открытая полусфера отверстием по потоку	0.35
Шар	0.20
Хорошо обтекаемое тело	0.05

Получим формулу для предельной скорости при падении тела, если для учета сопротивления движению используется формула гидравлического сопротивления. При установившемся движении равнодействующая всех действующих на тело сил равна нулю, откуда следует

,

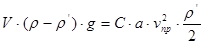и

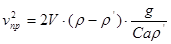. (12)

Пренебрегать плотностью среды в числителе формулы (12) можно только в случае

газовых сред, когда 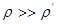, но для движения массивного тела, например, в воде такое пренебрежение приведет к ощутимой ошибке. Оценки показывают, что применение формулы гидравлического сопротивления справедливо для расчета движения реальных макроскопических тел в реальных средах.