Обобщим уравнение (9) на случай многокомпонентной фильтрации. Предполагается, что фазы (вода и нефть) не смешиваются, и пассивная примесь может иметь ненулевую концентрацию 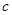 только в воде и на стенках пор. Концентрация воды во флюиде равна
только в воде и на стенках пор. Концентрация воды во флюиде равна 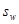 . Поле скоростей фильтрации воды равно
. Поле скоростей фильтрации воды равно 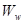 . Тогда поле скоростей течения воды определено в тех точках, где вода присутствует, и равно
. Тогда поле скоростей течения воды определено в тех точках, где вода присутствует, и равно
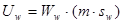 .
.
Рассмотрим произвольный объём 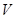 пористой среды. Закон сохранения количества примеси для этого объёма имеет вид:
пористой среды. Закон сохранения количества примеси для этого объёма имеет вид:
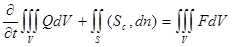 , (10)
, (10)
где:
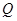 — концентрация примеси;
— концентрация примеси;
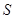 — граница объёма
— граница объёма 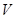 ;
;
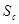 — плотность потока примеси;
— плотность потока примеси;
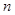 — нормаль к поверхности
— нормаль к поверхности 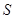 ;
;
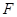 — плотность мощности источников примеси.
— плотность мощности источников примеси.
Рассмотрим малый объём 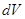 . Количество растворённой примеси в объёме
. Количество растворённой примеси в объёме 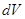 равно
равно 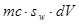 . Часть
. Часть 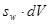 объёма
объёма 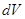 занята водой. Соответственно в этой части объёма имеем
занята водой. Соответственно в этой части объёма имеем 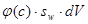 молей примеси, адсорбированной на стенках пор. Так как примесь может иметь ненулевую концентрацию только в воде, то она не сможет из адсорбированного состояния перейти в нефть. Поэтому в части объёма, занятой нефтью, плотность адсорбированной примеси будет такая же, как и в части объёма, заполненной водой. В итоге во всём объёме
молей примеси, адсорбированной на стенках пор. Так как примесь может иметь ненулевую концентрацию только в воде, то она не сможет из адсорбированного состояния перейти в нефть. Поэтому в части объёма, занятой нефтью, плотность адсорбированной примеси будет такая же, как и в части объёма, заполненной водой. В итоге во всём объёме 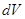 имеем
имеем 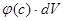 молей адсорбированной примеси.
молей адсорбированной примеси.
Тогда суммарное количество примесей в объеме 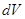 равно
равно
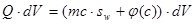 . (11)
. (11)
Рассмотрим некоторую малую площадь 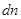 в пористой среде. Так как примесь может передвигаться только в воде, то достаточно рассмотреть поток через занятую водой часть
в пористой среде. Так как примесь может передвигаться только в воде, то достаточно рассмотреть поток через занятую водой часть 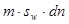 этой площади.
этой площади.
Конвективный поток будет равен
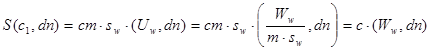 .
.
Диффузионный поток будет равен
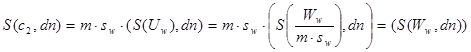 .
.
Тогда суммарный поток примеси через площадь 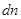 будет равен
будет равен
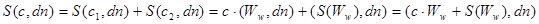 . (12)
. (12)
Закон сохранения массы (10) с учетом (11) и (12) запишется в виде
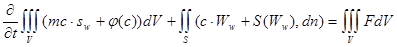 .
.
Отсюда
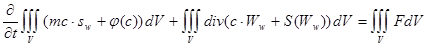 . (13)
. (13)
Так как объём 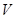 не зависит от времени, можно поменять местами дифференцирование по времени и интегрирование в первом слагаемом. Тогда, в силу произвольности
не зависит от времени, можно поменять местами дифференцирование по времени и интегрирование в первом слагаемом. Тогда, в силу произвольности 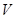 , будем иметь:
, будем иметь:
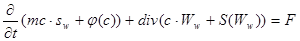 , (14)
, (14)
где:
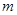 — пористость;
— пористость;
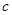 — концентрация примеси;
— концентрация примеси;
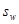 — водонасыщенность;
— водонасыщенность;
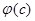 — концентрация адсорбированной в порах примеси;
— концентрация адсорбированной в порах примеси;
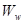 — скорость фильтрации воды;
— скорость фильтрации воды;
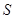 — диффузионный поток, вызванный конвективной диффузией;
— диффузионный поток, вызванный конвективной диффузией;
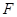 — плотность мощности источников примесей.
— плотность мощности источников примесей.
Скорость фильтрации воды 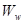 может быть определена в соответствии с обобщённым законом Дарси:
может быть определена в соответствии с обобщённым законом Дарси:
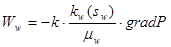 . (15)
. (15)
 2014-02-09
2014-02-09 599
599








