Для ламинарного режима (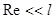 ) и шарообразной формы тела аналитическая формула для силы сопротивления получена ученым Стоксом и носит название формулы Стокса:
) и шарообразной формы тела аналитическая формула для силы сопротивления получена ученым Стоксом и носит название формулы Стокса:
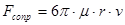 , (9)
, (9)
где 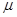 - коэффициент динамической вязкости среды;
- коэффициент динамической вязкости среды; 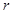 - радиус шара;
- радиус шара; 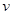 - его скорость относительно потока среды. Итак, формула, или закон, Стокса получена для медленного поступательного движения шара в неограниченной вязкой среде. Законом Стокса пользуются в коллоидной химии, молекулярной физике, физике аэрозолей. По закону Стокса можно определить скорость осаждения мелких капель тумана, частиц ила, коллоидных и аэрозольных частиц. Условие его применения:
- его скорость относительно потока среды. Итак, формула, или закон, Стокса получена для медленного поступательного движения шара в неограниченной вязкой среде. Законом Стокса пользуются в коллоидной химии, молекулярной физике, физике аэрозолей. По закону Стокса можно определить скорость осаждения мелких капель тумана, частиц ила, коллоидных и аэрозольных частиц. Условие его применения: 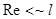 .
.
Определим предельную скорость при падении частицы, если сила сопротивления определяется формулой Стокса.
Сила тяжести равна 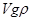 , где
, где 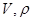 - объем и плотность материала частицы; подъемная сила равна
- объем и плотность материала частицы; подъемная сила равна 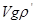 , где
, где 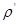 - плотность среды. Подъемная сила и сила сопротивления направлены противоположно скорости падения, а для установившегося движения сумма всех действующих сил равна нулю. Отсюда
- плотность среды. Подъемная сила и сила сопротивления направлены противоположно скорости падения, а для установившегося движения сумма всех действующих сил равна нулю. Отсюда
 .
.
Подставив выражение для объема частицы 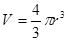 , получим
, получим
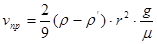 . (10)
. (10)
Если речь идет о падении шарика в воздухе, то плотностью воздуха можно пренебречь по сравнению с плотностью материала шарика, однако при падении в более плотных средах (например, в воде) формулу (10) следует использовать в полном виде. Порядки величин динамической вязкости для разных сред таковы:
| Среда | 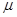 , мПа·с , мПа·с |
| Воздух | 0.0182 |
| Вода | 1.002 |
| Глицерин |
Оценки показывают, что при расчете скорости падения в воздухе формула Стокса справедлива лишь для частиц микронных размеров.
 2014-02-09
2014-02-09 8091
8091
