Определение поверхности теплообмена

Необходимая поверхность теплообмена выпарного аппарата определяется из уравнения теплопередачи

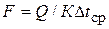(3.12)

в зависимости от тепловой нагрузки Q. Температурный напор 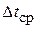принимается равным разности температур насыщения греющего пара t _п и кипения раствора t _кип:

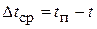_кип (3.13)

Температура кипения раствора находиться по уравнению

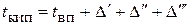, (3.14)

где 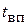- температура вторичного пара, определяемая по рабочему давлению в сепарационном пространстве аппарата. Температурные потери 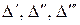определяются по методике изложенной в 2-м разделе.

Коэффициент теплопередачи К, 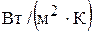, рассчитывается обычным способом; он зависит главным образом от удельной тепловой нагрузки, от температуры и концентрации раствора. С понижением температуры раствора и повышением его концентрации возрастает вязкость и уменьшается коэффициент теплопередачи.

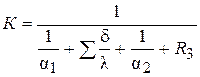, (3.15)

где δ, λ – толщина, м, и коэффициент теплопроводности, 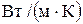, стенки трубы и загрязнений; R ₃ – термическое сопротивление загрязнений (накипи) поверхности труб, .

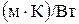Коэффициент теплоотдачи от конденсирующегося пара к поверхности нагревательных труб α₁ определяют по формуле

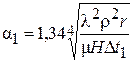, (3.16)

где Н – высота вертикальных труб в аппарате, м; 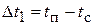- разность температур конденсирующегося пара и стенки; коэффициент динамической вязкости μ, 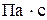, теплопроводность λ, 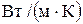, конденсата, его плотность ρ, кг/м³, выбираются при определяющей температуре насыщения 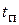; r - удельная теплота конденсации пара, Дж/кг.

Теплоотдача при кипении растворов еще недостаточно изучена. При кипении водных растворов можно принять удельную тепловую нагрузку аппаратов с естественной циркуляцией q =200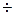0050000 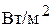, с принудительной циркуляцией q = 40 000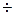80 000 .

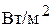В условиях работы выпарных установок на заводах наблюдается чаще всего пузырьковое кипение при средних тепловых нагрузках.

Коэффициент теплоотдачи от стенки к кипящему раствору для пузырькового кипения в вертикальных трубах при условии естественной циркуляции раствора определяется по уравнению

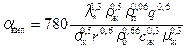, (3.17)

где λ_ж - теплопроводность раствора, 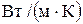; ρ_ж и ρ_п – плотности жидкости и пара, кг/м³, ρ₀ – плотность пара при р= 0,098 МПа, кг/м³; σ_ж - поверхностное натяжение раствора, Н/м; r - скрытая теплота парообразования, Дж/кг; с _ж - удельная теплоемкость раствора,; 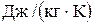μ_ж - динамическая вязкость раствора, 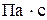; q - плотность теплового потока, .

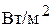Физико-химические параметры выбираются для растворов при температуре кипения. Уравнение (3.17) справедливо при q =400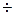0080000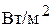; числе Pr_ж =0,8-100; давлении Р =(0,098-70,5) 10⁵ Па. Это уравнение дает удовлетворительные результаты при соблюдении оптимального уровня жидкости в трубах выпарного аппарата:

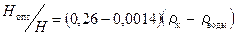, (3.18)

где Н – высота теплообменных труб, м, ρ_воды- плотность воды, кг/м³.

В аппаратах с вынесенной зоной кипения, а также в аппаратах с принудительной циркуляцией обеспечиваются высокие скорости движения растворов в трубках грею­щей камеры, и вследствие этого — устойчивый турбулентный режим течения. Принимая во внимание, что разность температур теплоносителей (греющего пара и кипя­щего раствора) в выпарном аппарате невелика, для вычисления коэффициентов теплоотдачи со стороны жидкости используют эмпирическое уравнение [3]:

Nu=0,023Re^0,8 Pr^0,4. (3.19)

Физические характеристики растворов, входящие в числа подобия, находят при средней температуре потока.

При кипении растворов в пленочных выпарных аппаратах коэффициент тепло­отдачи рекомендуется [7] определять по уравнению

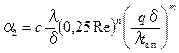, (3.20)

где λ— теплопроводность кипящего раствора, 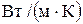; δ — толщина пленки, в м, рассчитываемая по уравнению

,

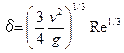где v — кинематическая вязкость раствора, м²/с; Re = 4 Г/μ — критерий Re для пленки жидкости; Г =G_j/ П— линейная массовая плотность орошения, 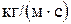; G_j — расход раствора, поступающего в j -й корпус, кг/с; П = π d _вн n=F _cp /H — смоченный периметр, м; μ —вязкость кипящего раствора, Па·с; q — тепловая нагрузка, которую в расчете принимают равной α₁Δ t ₁, Вт/м², t _в.п- температура вторичного пара.

Значения коэффициентов и показателей степеней в уравнении (3.20):

при q < 20 000 Вт/м²: c =163,1; n= - 0,264; m =0,685;

при q > 20 000 Вт/м²: c = 2,6; n = 0,203; m =0,322.

Коэффициент теплопередачи определяется как

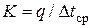
Значение коэффициента теплопередачи может быть найдено следующим образом.

Для установившегося процесса передачи теплоты от пара через стенку к раствору справедливо уравнение

,

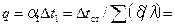
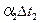где Δ t ₁— разность температур конденсации греющего пара и стенки; Δ t _ст — разность температур между поверхностями стенки; Δ t ₂— разность между температурой стенки со стороны раствора и температурой кипения раствора.

Распределение температур в процессе теплопередачи от пара через стенку к кипящему раствору показано на рис. 3.2.

Задаваясь величиной Δ t ₁ и определив коэффициент теплоотдачи α₁, вычисляют удельную тепловую нагрузку в процессе передачи теплоты от конденсирующегося пара к стенке:

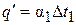. (3.21)

Величина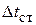 определяется как

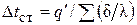. (3.22)

Тогда

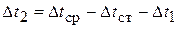, (3.23)

Удельная тепловая нагрузка в процессе передачи теплоты от стенки к раствору

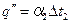, (3.24)

Если q' 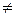q", принимаем новое значение Δ t ₁ и повторяем расчет до сходимости величин q' и q". Расхождение между удельными тепловыми нагрузками не должно превышать 3 %.

Обычно выполняют 2—3 приближения, а затем строят графическую зависимость удельной тепловой нагрузки q' и q" от Δ t _1. В точке пересече­ния линий q' = f (Δ t ₁)и q" = f (Δ t ₁) определяется значение величины Δ t ₁.

Далее коэффициент теплопередачи К рассчитывается по уравнению (3.12).

При расчете аппаратов со свободной, естественной и прину­дительной циркуляцией параметры кипящей жидкости берут при конечной концентрации раствора.