2014-02-09
5679
Все вещества являются магнетиками – при помещении их во внешнее магнитное поле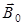 
они создают свое магнитное поле 
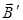, то есть намагничиваются:
|
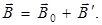
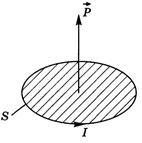
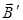магнетика можно пояснить на основе гипотезы Ампера существовании внутри молекул молекулярных токов (микротоков). Произведение кругового тока на обтекаемую им площадь называют магнитным моментом (рис. 9.5) 
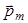. Модуль вектора 
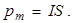Для характеристики магнетика вводят вектор намагничивания 
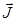, который равен векторной сумме магнитных моментов 
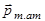атомов, находящихся в единице объема вещества: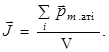 
Ориентация магнитных моментов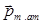 
атомов во внешнем магнитном поле и создает не равное нулю магнитное поле 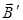вещества и соответственно 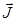(рис. 9.6).
|
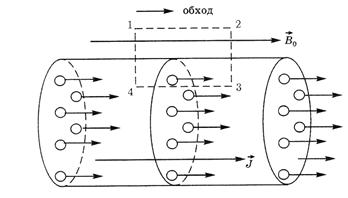
Для удобства описания магнитных полей в среде вводится вектор напряженности магнитного поля
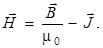
В случае вакуума 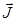= 0,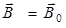 
и поэтому
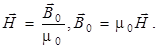
Для однородных изотропных магнетиков из опыта установлена следующая формула связи векторов 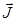и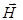
:
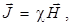
где χ – магнитная восприимчивость вещества.
Для векторов 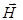и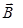 
в случае однородного и изотропного магнетика с учетом выше приведенных формул получаются следующие выражения:
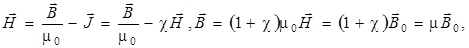
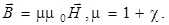
Теорему о циркуляции вектора 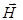по произвольному замкнутому контуру Г можно представить в виде
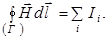
По магнитным свойствам вещества можно разбить на три группы: диамагнетики, парамагнетики и ферромагнетики.
Диамагнетиками называются вещества, магнитные моменты атомов или молекул которых при отсутствии внешнего магнитного поля равны нулю. При внесении диамагнитного вещества в магнитное поле в каждом атоме наводится магнитный момент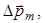 
направленный противоположно вектору 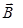магнитной индукции поля. Для диамагнитных веществ χ < 0 и μ < 1.
У парамагнитных веществ магнитные моменты атомов или молекул при отсутствии внешнего магнитного поля не равны нулю. При внесении парамагнетика в магнитное поле магнитные моменты атомов стремятся сориентироваться по направлению этого поля. Для парамагнитных веществ χ > 0 и μ > 1. Эксперименты указывают, что μ пара- и диамагнитных веществ незначительно отличаются от единицы.
Ферромагнитными веществами называют такие вещества, в которых внутреннее магнитное поле в сотни и тысячи раз превышает вызвавшее его внешнее поле.
Объемная плотность энергии магнитного поля в неферромагнитной среда равна
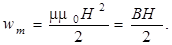
Лекция 10
