Рисунок 3.5
Ввиду того, что 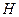 <<
<< 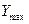 начальным участком можно пренебречь.
начальным участком можно пренебречь.
Рассмотрим подробнее характер влияния скорости встречи на полную глубину проникания.
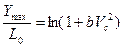 (3.19)
(3.19)
Очевидно, что при 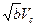 <<1
<<1
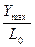 @
@ 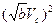 (3.20)
(3.20)
а при 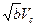 >>1
>>1
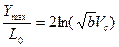 (3.21)
(3.21)
Таким образом глубина проникания 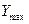 при малых скоростях встречи пропорциональна квадрату скорости встречи, а при больших – логарифму скорости встречи.
при малых скоростях встречи пропорциональна квадрату скорости встречи, а при больших – логарифму скорости встречи.
ln(1 + bV2c)


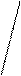


 Ymax K (Ö bVc)
Ymax K (Ö bVc)

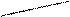
 Lo
Lo

 (Ö b V2c)
(Ö b V2c)
 | 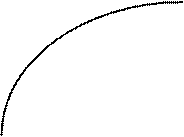 | ||
 |
1 2ln(Ö b Vc)
 |

 0 1 2 3 Ö b Vc
0 1 2 3 Ö b Vc
Рисунок 3.6
Как следует из графиков рисунка 3.6 с достаточной для практики точностью при 0,5 £ 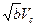 £ 3,5 зависимость может быть представлена прямой линией
£ 3,5 зависимость может быть представлена прямой линией
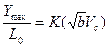 дставляя в это уравнение значение
дставляя в это уравнение значение 
 и имея в виду, что
и имея в виду, что 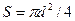 получим
получим 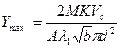 . Обозначим
. Обозначим 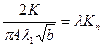
тогда 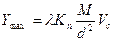 (3.22)
(3.22)
где 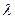 - коэффициент, зависящий от формы головной части,
- коэффициент, зависящий от формы головной части, 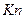 – коэффициент проникания, зависящий от свойств среды.
– коэффициент проникания, зависящий от свойств среды.
В таком виде формула была получена по результатам обработки экспериментальных стрельб, проведенных на острове Березань. Эта формула получила название “Березанской.”
Значения 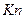 и
и 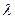 приведены в табл. 3.4, 3.5.
приведены в табл. 3.4, 3.5.
Таблица 3.4
| Среда | 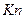 | Среда | 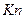 |
| Песок | 4,5´10-6 | Гранит | 1,6´10-6 |
| Глина | 7,0´10-6 | Сосна, ель | 5,0´10-6 |
 Известняк Известняк | 2,0´10-6 | Бетон высшего качества | 0,8´10-6 |
| Бетон среднего качества | 1,2´10-6 |
Таблица 3.5
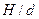 | 0…0,5 | 0,5…1,0 | 1,0…1,5 | 1,5…2,0 |
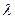 | 1,0 | 1,1 | 1,25 | 1,40 |
Пример: определить глубину и время проникания АБ ФАБ-500-М62.
Грунт – глина; 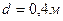 ;
; 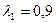 ;
; 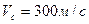
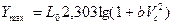
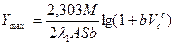
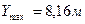
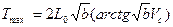
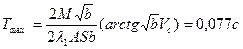
 Vc
Vc
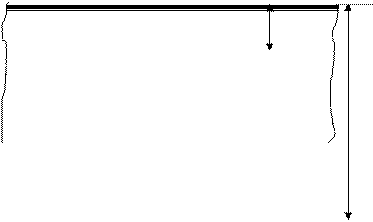 |
 V1 h1
V1 h1

V2 h2
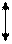

 Ymax
Ymax
V3 h3
 |
V=0
 Рисунок 3.7
Рисунок 3.7
Для определения возможности пробития многослойных преград необходимо определить конечную скорость после пробития первого слоя 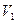 по зависимости
по зависимости

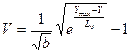 или
или
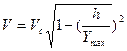 (3.33)
(3.33)
По зависимости 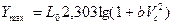 определяется максимальная толщина пробиваемой первой преграды с параметрами
определяется максимальная толщина пробиваемой первой преграды с параметрами 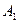 и
и 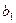 . Затем определяется величина
. Затем определяется величина 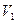 , которая является начальной скоростью для пробития второй преграды. Затем цикл расчета повторяется для второй преграды и т.д. В конечном итоге
, которая является начальной скоростью для пробития второй преграды. Затем цикл расчета повторяется для второй преграды и т.д. В конечном итоге 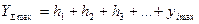
 2014-02-09
2014-02-09 1112
1112








