Центральным растяжением (сжатием) называют такой вид деформации, при котором в поперечных сечениях бруса возникают только продольные силы 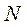 , для определения которых достаточно условий статического равновесия.
, для определения которых достаточно условий статического равновесия.
Растягивающие продольные силы считаются положительными, а сжимающие – отрицательными.
На рис. 4.3,а представлена схема бруса, нагруженного осевыми силами. Для контроля правильности расчета продольных сил определим реакцию R в заделке, направив ее на растяжение по отношению к брусу. Используя уравнение равновесия и выбрав положительное направление продольной оси бруса 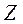 , получим
, получим
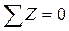 ;
; 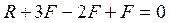 ;
; 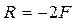 .
.
Минус в ответе означает, что реакция направлена не на растяжение, как мы выбрали, а на сжатие.
Для определения продольных сил применим метод сечений:
Разбиваем брус на силовые участки I, II, III. Проводим на каждом участке произвольные поперечные сечения и отбрасываем части бруса.
Заменяем действие отброшенных частей бруса на оставшиеся на каждом участке неизвестными продольными силами 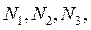 направив их от сечений, т.е. на растяжение (рис. 4.3, б, в, г).
направив их от сечений, т.е. на растяжение (рис. 4.3, б, в, г).
Для каждого из участков составляем уравнение равновесия:
Участок I (рис. 4.3, б) 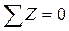 ;
; 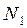
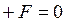 ;
; 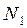 = -
= - 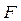 ;
;
Участок II (рис. 4.3, в) 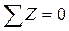 ;
; 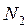
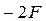
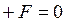 ;
; 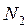 =
= 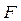 ;
;
Участок III (рис. 4.3, г) 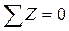 ;
; 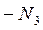 +
+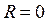 ;
; 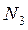 =
= 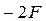 .
.
Отсюда имеем 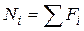 , т.е. продольная сила
, т.е. продольная сила 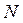 в произвольном сечении бруса численно равна алгебраической сумме проекций на продольную ось всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.
в произвольном сечении бруса численно равна алгебраической сумме проекций на продольную ось всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.
Это вывод позволит нам в дальнейшем определять продольные силы 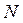 без использования описанной процедуры составления уравнений равновесия. Так, например, для участка II получаем
без использования описанной процедуры составления уравнений равновесия. Так, например, для участка II получаем
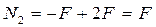 .
.
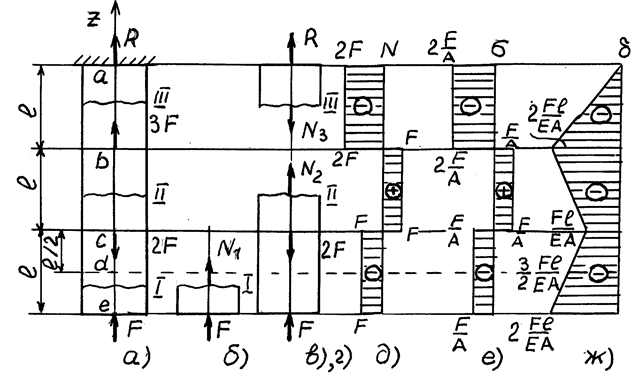 Рис. 4.3 Рис. 4.3 |
По полученным данным строим график распределения продольных сил по длине бруса – эпюрупродольных сил (рис. 4.3, д). для построения эпюры проводим базовую линию (ось бруса), и выбрав масштаб, откладываем на каждом участке величины продольных сил. Т.к. на схемах рис. 4.3, б, в, г продольные силы были направлены на растяжение, то знаки в ответах поле решений уравнений равновесия указывают: (+) – растяжение,
(-) – сжатие. На эпюрах проставляют значения найденных продольных сил, их знак и наносят штриховку перпендикулярно оси бруса.
Из анализа эпюры 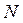 вытекает следующее правило ее проверки: в поперечных сечениях бруса, в которых приложены внешние активные (
вытекает следующее правило ее проверки: в поперечных сечениях бруса, в которых приложены внешние активные (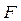 ) или реактивные (
) или реактивные (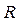 ) силы, на эпюре продольных сил возникают скачки, равные по величине этим нагрузкам.
) силы, на эпюре продольных сил возникают скачки, равные по величине этим нагрузкам.
 2014-02-09
2014-02-09 3340
3340
