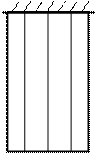
Задача определения напряжений является статически неопределимой задачей, т.к. неизвестен закон распределения внутренних усилий по площади сечения. Опыт показывает, что прицентральном растяжении, сжатии строго выполняется гипотеза плоских сечений: поперечные сечения бруса плоские и перпендикулярные к оси (рис. 3.2, а) до деформации остаются плоскими и перпендикулярными к оси после деформации (рис. 3.2, б). Такая картина деформаций позволяет считать, что в поперечных сечениях бруса действуют только нормальные напряжения, равномерно распределенные по сечению (σ = const), а касательные напряжения равны нулю. В этом случае нормальная сила N (рис.3.2, в) является равнодействующей нормальных напряжений в поперечном сечении: N=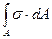 . Так как σ = const, то N=σA, откуда следует формула для нормальных напряжений при центральном растяжении или сжатии:
. Так как σ = const, то N=σA, откуда следует формула для нормальных напряжений при центральном растяжении или сжатии: 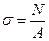 , здесь А – площадь поперечного сечения бруса.
, здесь А – площадь поперечного сечения бруса.
При растяжении σ > 0, при сжатии σ < 0, т.е., знак напряжений определяется знаком N.

В продольных сечениях (параллельных оси бруса) напряжения отсутствуют. На наклонных площадках действуют и нормальные и касательные напряжения.
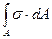 . Так как σ = const, то N=σA, откуда следует формула для нормальных напряжений при центральном растяжении или сжатии:
. Так как σ = const, то N=σA, откуда следует формула для нормальных напряжений при центральном растяжении или сжатии: 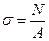 , здесь А – площадь поперечного сечения бруса.
, здесь А – площадь поперечного сечения бруса.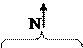








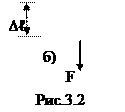
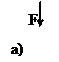
 2014-02-02
2014-02-02 2213
2213
