2014-02-09
3974
Под действием силы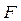 
брус длиной 
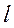удлиняется на величину 
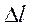, которую называют полным или абсолютным удлинением (при сжатии – укорочением) (рис.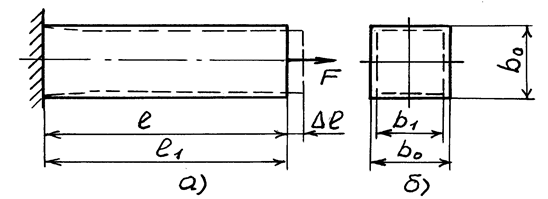4.5).
 Рис. 4.5 |
Из рассмотрения рисунка види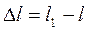м
[м].
При растяжении 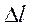>0, при сжатии 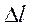< 0.
Так как согласно гипотезе плоских сечений Бернулли по всей длине в любой точке поперечного сечения бруса возникают одинаковые удлинения то и линейные деформации будут одинаковы и равны
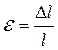или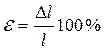 
.
При растяжении (или сжатии) бруса меняются и его поперечные размеры. Из рис. 4.5, б абсолютное сужение бруса:
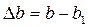[м].
Причем, при растяжении бруса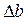 
< 0, а при сжатии - 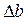>0. Тогда относительная поперечная деформация:
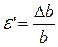или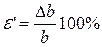 
.
Опыт показывает, что в пределах применимости закона Гука при растяжении (сжатии) поперечная деформация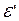 
прямо пропорциональна продольной деформации 
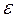, но имеет обратный знак:
.
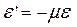Коэффициент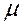 
называется коэффициентом Пуассона. На основании формулы принимают:
.
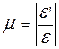Коэффициент Пуассона изменяется в пределах 0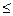
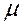
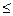0,5 и для каждого материала является постоянной величиной, характеризующей упругие свойства материала. Например: для пробки 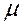= 0; для сталей 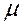= 0,25 ÷ 0,30; для резины и парафина 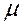= 0,5.
В 1660 г. английский ученый Р. Гук вывел закон, который в настоящее время формулируется так: деформация прямо пропорциональна вызвавшему ее напряжению, т.е.
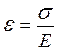или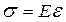 
; 
.
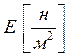Величину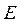 
называют модулем продольной упругости (модулем Юнга). Это физическая величина постоянная материала, характеризующая его упругость. Чем больше значение 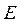, тем меньше, при прочих равных условиях (нагрузке, длине, площади), продольная деформация бруса, т.е. тем материал жестче.
