Усилия и напряжения в поперечном сечении бруса

Растяжение и сжатие весьма часто встречаются в элементах строительных конструкций и машин.

Если внутренние силы в поперечном сечении стержня сводятся только к одному силовому фактору – продольной силе N, а все остальные внутренние силы равны нулю, то имеет место центральное растяжение или сжатие.

Внешние силы, вызывающие растяжение или сжатие, приложенные к концевым или промежуточным сечениям стержня, должны быть также направлены по его оси или приводиться к равнодействующей, направленной по этой оси.

Рассмотрим растянутый стержень (рис.2.1). Передача сил Р на этот стержень может быть осуществлена различными способами: можно, например, отогнуть концы стержня и захватить его за образовавшуюся петлю, можно изготовить стержень с бортиками и передать усилия через выступ, можно нарезать резьбу, можно сделать отверстие и в отверстие вставить палец, словом, вариантов можно предложить много. Всем этим, отличающимся друг от друга конструкциям, может быть поставлена в соответствие одна и та же расчётная схема (рис.2.2). Это возможно благодаря справедливости принципа Сен-Венана, названному по имени предложившего его французского учёного, сыгравшего большую роль в создании сопротивления материалов и теории упругости в середине XIX века.

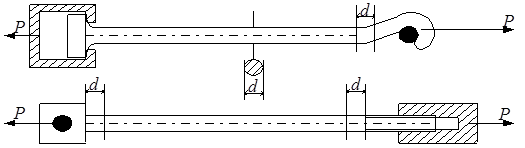
Рис.2.1

Принцип Сен-Венана утверждает следующее: особенности приложения внешних сил сказываются на расстоянии, не превышающем характерный размер поперечного сечения. Напряжения и деформации в стержне на достаточном удалении от мест захвата (равном характерному размеру поперечного сечения – диаметру d) будут одинаковы, если одинаковы приложенные силы. Применение принципа Сен-Венана позволяет существенно расширить общность основных расчётных формул сопротивления материалов, поскольку освобождает от необходимости учитывать конкретные особенности местного распределения сил.

Для определения продольных сил применяется метод сечений, который заключается в том, что стержень мысленно пересекается плоскостью, перпендикулярной оси стержня, на две части. Продольная сила N равна сумме проекций на ось стержня сил, действующих по одну сторону от сечения. Сила N считается положительной, если она вызывает растяжение (направлена от сечения), и отрицательной, если она вызывает сжатие (направлена к сечению).

Рассмотрим расчётную схему стержня (рис.2.2). Стержень рассекаем сечением m-n и рассматриваем равновесие левой отсечённой части. Целесообразно неизвестную продольную силу N принимать положительной (растягивающей). Если при решении уравнения статики сила N получится со знаком “–“, то её направление надо поменять на противоположное и учитывать в дальнейшем расчёте, что стержень сжат. В нашем случае (рис.2.2.) получим N = P, т.е. стержень растянут: ∑x = 0, N – P = 0, N = P.

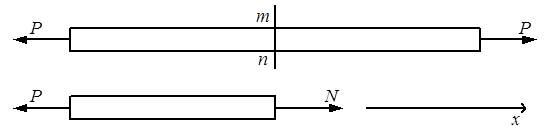
Рис.2.2.

В более сложных случаях нагружения стержня имеет смысл строить график изменения продольных сил по длине, называемый эпюрой продольных сил. На рис.2.3 изображен брус, находящийся под действием внешних сил, направленных вдоль оси. Показана эпюра продольных сил.

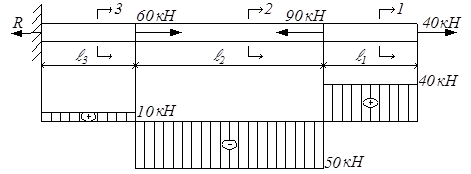
Рис.2.3

При построении эпюры N рассматривали равновесие отсечённых частей на каждом из участков ℓ₁, ℓ₂, ℓ₃ (рис.2.4).

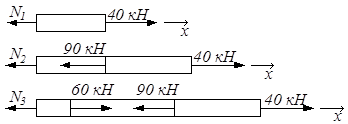
∑х = 0: 40 – N1 = 0, N1 = 40 кН; ∑х = 0: 40 – 90 – N2 = 0, N2 = – 50 кН; ∑х = 0: 40 – 90 + 60 – N3 = 0, N3 = 10 кН.

Рис.2.4

Из рис.2.4 следует, что мы все время рассматривали равновесие правой отсечённой части. Это связано с тем обстоятельством, что мы не определили реакцию опоры R, которая относится к внешним силам. Если бы сначала нашли R из уравнения статики, можно было бы рассматривать равновесие и левой отсечённой части. Построив эпюру N, получили R = 10 кH (растяжение).

С помощью построенной эпюры легко установить значение N, необходимое для расчёта на прочность. Так, в нашем примере получили½N_max½ = 50кН. Это значение не совпадает ни с одной из внешних сил.

Продольная сила N, возникающая в поперечном сечении бруса, представляет собой равнодействующую внутренних нормальных сил, распределённых по площади поперечного сечения и связана с возникающими в этом сечении нормальными напряжениями зависимостью:

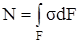, (2.1)

где σ – нормальное напряжение в произвольной точке поперечного сечения, принадлежащей элементарной площадке dF;

F – площадь поперечного сечения бруса.

Однако из формулы (2.1) нельзя найти закон распределения нормальных напряжений σ по площади поперечного сечения. Опыты показывают, что если нанести на поверхность бруса систему взаимно перпендикулярных линий (рис.2.5), то после нагружения поперечные линии a-a, b-b, c-c, d-d переместятся параллельно самим себе.

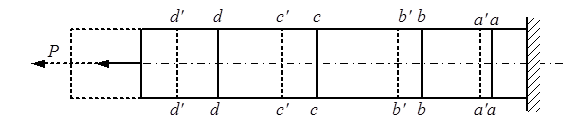
Рис 2.5.

Каждую такую линию можно рассматривать как след плоскости поперечного сечения бруса, – это позволяет считать, что поперечные сечения бруса, плоские до его нагружения, остаются плоскими и при действии нагрузки. Выполняется гипотеза плоских сечений, впервые предложенная голландским учёным Д. Бернулли и широко применяемая в задачах сопротивления материалов: удлинения и напряжения во всех точках поперечного сечения бруса равны между собой, что позволяет в выражении (2.1) вывести величину σ за знак интеграла. Таким образом,

,

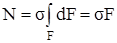откуда

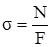. (2.2)

Итак, в поперечных сечениях бруса при его растяжении (или сжатии) возникают равномерно распределённые нормальные напряжения, равные отношению продольной силы к площади поперечного сечения.