Импеданс цепи переменного тока с последовательным включением резистора, катушки и конденсатора. Резонанс напряжений

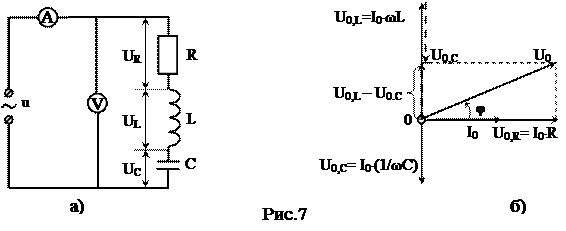
Рассмотрим цепь, состоящую из резистора R, катушки индуктивности L и конденсатора C (рис.7а). Подадим на концы этой цепи переменное напряжение u = U₀cosωt. В цепи возникнет переменный ток той же частоты ω, амплитудой I₀ и фазой φ, значение которой будет определяться параметрами цепи: сопротивлением R, индуктивностью L и электроёмкостью С. Этот ток вызовет падения напряжений на отдельных элементах участка цепи – U_0,R, U_0,C, U_0,L. Поскольку соединение последовательное, то результирующее напряжение U₀ будет определяться векторной суммой напряжений на отдельных элементах (рис.7б). По теореме Пифагора получим:

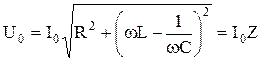. (14)

Закон Ома для данной цепи запишется так:

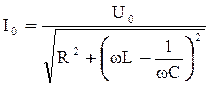, (15)

где 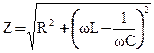– полное сопротивление или импеданс цепи переменного тока. Треугольник сопротивлений представлен на рис. 8.

Разность фаз между током I и напряжением U определяется углом φ между векторами U₀ и I₀. Из диаграммы (рис.8) следует:

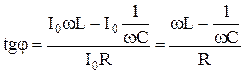. (16)

Из формулы для Z вытекает, что чем ближе по величине 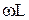и 1/ωС, тем меньше полное сопротивление Z и тем больше ток в цепи. При ωL = 1/ωC угол сдвига фаз обращается в нуль (φ = 0), полное сопротивление Z = R и ток достигает максимального значения:

I_0,max = U_0,рез / R. (17)

Это явление называется резонансом напряжения. Для цепи с заданными L и C, резонанс имеет место при частоте .

РАБОТА И МОЩНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Мгновенное значение мощности р(t) переменного тока равно произведению мгновенных значений напряжения u(t) = U₀cosωt и силы тока i (t) = I₀ cos(ωt – φ):

р(t) = U₀cosωt×I₀ cos(ωt – 90⁰) = I₀U₀ cosωt× cos(ωt – 90⁰).()

Воспользовавшись формулой 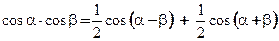получим:

.

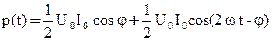Практический интерес представляет среднее по времени значение мощности Р. Т.к. среднее значение cos(2ωt - φ) равно нулю, то

.()

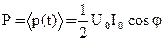Из векторной диаграммы рис. 7б следует, что U₀ cosφ = R I₀. Поэтому 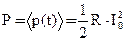. Такую же мощность развивает постоянный ток, силой 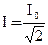. Это значение называется действующим (или эффективным) значением силы переменного тока. Аналогично величина 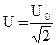называется действующим (или эффективным) значением напряжения. С использованием действующих (или эффективных) значений тока и напряжения Р = U₀ I₀cosφ.Множитель cosφ называется коэффициентом мощности. Как видно из диаграммы рис. 7б, при равенстве реактивных значений сопротивлений Х_C = Х_L множитель cosφ = 1 (φ = 0) Р = U₀ I₀, т.е. выделяющаяся в цепи мощность имеет максимальное значение. При чисто реактивном сопротивлении цепи (R = 0) мощность, выделяемая в цепи, равна нулю. По этой причине на практике электрическую цепь переменного тока стремятся сбалансировать так чтобы значения реактивных сопротивлений Х_C и Х_L были как можно ближе. Для промышленных установок наименьшее допустимое значение cosφ = 0,85.

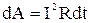или 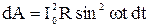. (48)

Работа за период T:

.

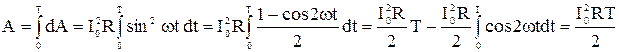(49)

Средняя мощность переменного тока 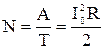. (50)

Обозначим , откуда эффективный (действующий) ток - 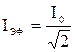.(51)

Тогда 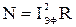. (52)

Из сравнения соотношений (47) и (52) следует, что эффективная сила переменного равна силе такого постоянного тока, который имеет ту же мощность, что и данный переменный ток.

Если в цепи переменного тока имеются реактивные сопротивления, то мощность:

(53)

(на основании тригонометрического тождества: ).

Среднее значение мощности N_С за период Т, а, следовательно, и за любой промежуток времени t>>T, равно разности средних значений. Но первый член есть постоянная величина, не зависящая от времени, а второй – периодическая функция, среднее значение которой за период T равна нулю. Таким образом, 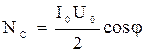(54)

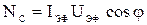или (55)

Множитель 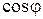называется коэффициентом мощности электрической цепи. Если R=0, то 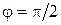и N_C=0. Энергия, которая поступает в цепь от источника за T/2, возвращается источнику в течение следующей половины периода. Следовательно, для повышения мощности, отдаваемой переменным током в цепь, необходимо добиться повышения 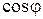путём включения в цепь таких R_L и R_C нагрузок, которые соответствуют условию резонанса (45).