Криволинейное движение

Угловая скорость и угловое ускорение.

Криволинейное движение.

Тема 1. Кинематика.

Лекция _№2.

3. Примеры расчёта кинематических характеристик автомобиля.

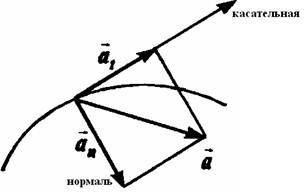
Пусть траектория точки – произвольная кривая.

Выберем на ней произвольную точку.

Вектор ускорения можно представить в виде суммы составляющих по двум взаимно перпендикулярным осям: касательной и нормали к кривой.

Определение 1.

Составляющая ускорения, направленная по касательной к траектории, носит название тангенциального ускорения – a_t, а направленная ей перпендикулярно — нормального ускорения – a_n.

Получим формулы, выражающие величины 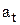и 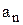через характеристики движения.

Очевидно, что 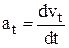и .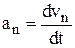

Модуль полного ускорения будет равен:

.

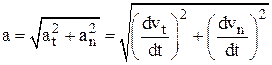Формулу для полного ускорения можно записать в более простом и наглядном виде.

При достаточно малых приращения скоростей также достаточно малы.

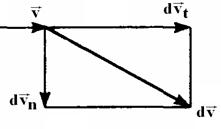
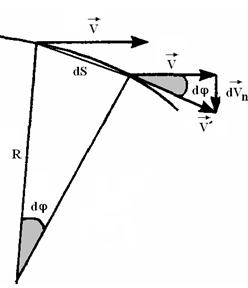При этом, как следует из рисунка, изменение скорости по величине определяется её касательной составляющей – 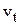и, соответственно, 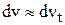, а изменение скорости по направлению – нормальной компонентой – .

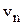Поэтому тангенциальное ускорение может быть записано как производная по времени от величины скорости (приближённо!):

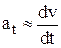. (11)

Найдем величину .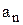

Возьмём наиболее простой случай криволинейного движения — равномерное движение по окружности, когда 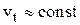. Рассмотрим перемещение точки за время , которому соответствует угол поворота – 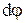по дуге 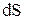окружности радиуса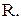

Треугольники с углом 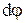оказываются подобными (как равнобедренные с равными углами при вершинах, напомним, что ).

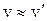Из подобия треугольников следует 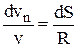, откуда находим выражение для нормального ускорения:

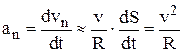. (12)

Формула для полного ускорения при движении по окружности принимает вид:

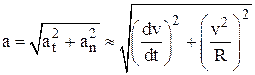. . (13)

ПРИМЕЧАНИЕ. Соотношения (11), (12) и (13) можно распространить на всякое криволинейное движение (не только для движения по окружности!). Это связано с тем, что всякий участок криволинейной траектории в достаточно малой окрестности точки всегда можно приближенно заменить дугой окружности.