Энтропия. Термин «энтропия» был введен Р

Термин «энтропия» был введен Р. Клаузиусом в 1865г. Энтропия также является функцией состояния

.

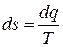Это выражение при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния. Энтропия обозначается для 1 кг газа через s и измеряется в Дж/(кг∙К). Для произвольного количества газа энтропия, равна S=Мs и измеряется в Дж/К.

Формула справедлива как для идеальных газов, так и для реальных тел.

Подобно любой другой функции состояния энтропия может быть представлена в виде функции любых двух параметров состояния:

S=F(Р,V); S=F(Р,T); S=F(V,T).

При температурах, близких к абсолютному нулю, все известные вещества находятся в конденсированном состоянии. В. Нернст (1906г.) экспериментально установил, а М. Планк (1912 г.) окончательно сформулировал следующий принцип: при температуре, стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю,
т.е. S_о= 0 при T = ОК. Этот закон называют третьим законом термодинамики или тепловой теоремой Нернста. Он позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии.

Аналитически значение энтропии для заданного состояния определяется интегрированием уравнения:

,

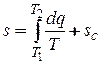где s_C — константа интегрирования.

Поделив все члены уравнения первой формы первого закона термодинамики на Т, получим

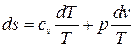
и, проинтегрировав, получим

s₂ – s₁ = .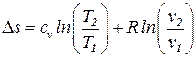

Энтропия применяется для расчёта неравновесных процессов, к которым относятся все процессы в реальных машинах. Это процессы, сопровождающиеся трением поршня или вихреобразованием в газе, или теплоотдачей в стенки. Неравновесность всегда приводит к росту энтропии, т.е. энтропия является мерой потерь или неравновесности. Поскольку в выражении энтропии температура находится в знаменателе, а потери сопровождаются снижением температуры, то в реальных неравновесных процессах энтропия увеличивается.