Точки разрыва функции

Рассмотрим функцию у = f (x), определённую на интервале ] a, b [, кроме, быть может, точки х ₀ Î ] a, b [.

Определение. Точка х ₀ называется точкой разрыва данной функ-ции, если в ней функция определена, но не является непрерывной, или не определена в этой точке.

Если х ₀ – точка разрыва функции f (x) и существуют конечные пределы f (х ₀ – 0) = 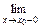f (х), f (х ₀ + 0) = 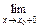f (х), то она называется точкой разрыва первого рода.

Величина f (х ₀ + 0) – f (х ₀ – 0) называется скачком функции f (x) в точке х ₀.

Пусть функция у = f (x) имеет разрыв в точке х ₀ и f (х ₀ + 0) = f (х ₀ – 0), тогда х ₀ называется точкой устранимого разрыва. Это название оправдано тем, что если доопределить такую функцию (если она не была определена в точке х ₀), положив f (х ₀) = 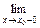f (х) = 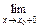f (х), то получится функция, непрерывная в точке х ₀.

Например, для функции f (x) = 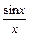точка х ₀ = 0 является точкой устранимого разрыва.

Если х ₀ – точка разрыва и, по крайней мере, один из пределов f (х ₀ + 0), f (х ₀ – 0) является бесконечным или не существует, то х ₀ называется точкой разрыва второго рода.

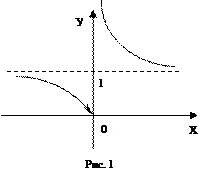
Например, 1) точка х ₀ = 0 – точка разрыва второго рода для функции f (x) = 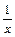, поскольку f (х ₀ – 0) = –¥, f (х ₀ + 0) = +¥; 2) так как f (х ₀ + 0) = +¥, то точка х ₀ = 0 является точкой разрыва второго рода для функции f (x) = 3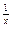(см. рис. 1).