Лекция № 5
ДОКУМЕНТАЦИОННОЕ ОБЕСПЕЧЕНИЕ УПРАВЛЕНИЯ
КОЛЬВА Николай Алексеевич
курс лекций
учебно-методическое пособие для студентов экономических специальностей
учебных заведений среднего профессионального образования
Литературный редактор – А.Н.Вылобков
Технический редактор – Н.А.Кольва
Издано в авторской редакции
Подписано в печать 2010-10-28
Бумага офисная. Гарнитура Arial Narrow
Усл.печ.л.15,25. Уч.-изд.л.14,18. Тираж 50 экз. Заказ № 691
_________________________________________________________________________
Отпечатано оперативными полиграфическими средствами учебного заведения
ФГОУ СПО «Донской государственный межрегиональный колледж
строительства, экономики и предпринимательства»
346400, г. Новочеркасск, Ростовской обл., пр. Платовский, д. 94, методкабинет, офис 24
Определение.
Функция 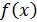 , определенная в некоторой окрестности точки
, определенная в некоторой окрестности точки 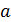 , называется непрерывной в точке
, называется непрерывной в точке 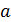 , если
, если
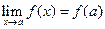 (1)
(1)
Таким образом функция непрерывна в точке 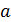 , если выполняются следующие условия:
, если выполняются следующие условия:
а) функция 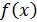 определена в некоторой окрестности точки
определена в некоторой окрестности точки 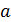 , то есть:
, то есть:
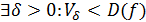
б) существует 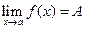 ;
;
в) 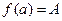 .
.
Определение непрерывности функции 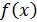 в точке
в точке 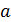 , выраженное в условии (1), можно сформулировать с помощью неравенств (на языке
, выраженное в условии (1), можно сформулировать с помощью неравенств (на языке 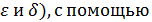 окрестностей и в терминах последовательностей в виде:
окрестностей и в терминах последовательностей в виде:
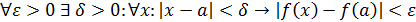 ;
;
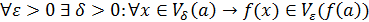 ;
;
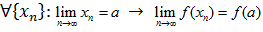 .
.
Подчеркнем, что в определении непрерывности в отличие от определения предела рассматривается полная, а не проколотая окрестность точки 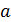 и пределом функции является значение этой функции в точке
и пределом функции является значение этой функции в точке 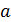 .
.
Назовем разность 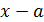 приращением аргумента и обозначим
приращением аргумента и обозначим 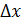 , а разность
, а разность 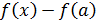 – приращением функции, соответствующей данному приращению аргумента
– приращением функции, соответствующей данному приращению аргумента 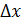 и обозначим его
и обозначим его 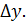
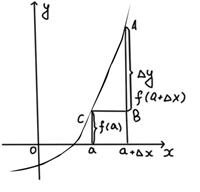
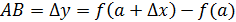 .
.
При этих обозначения (1) примет вид
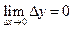 |
Таким образом непрерывность функции в точке означает, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Точки разрыва и их классификация
Пусть функция определена в некоторой проколотой окрестности точки 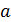 . Точку
. Точку 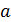 назовем точкой разрыва функции, если эта функция либо не определена в точке
назовем точкой разрыва функции, если эта функция либо не определена в точке 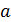 , либо определена, но не является непрерывной в точке
, либо определена, но не является непрерывной в точке 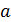 .
.
Следовательно, точка 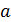 – точка разрыва функции, если не выполняется по крайней мере одно из следующих условий:
– точка разрыва функции, если не выполняется по крайней мере одно из следующих условий:
а) 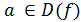 ;
;
б) Существует конечный предел 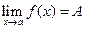 ;
;
в) 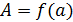 .
.
Если 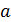 – точка разрыва функции, причем в этой точке существует конечный предел слева и справа, то есть
– точка разрыва функции, причем в этой точке существует конечный предел слева и справа, то есть
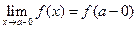 или
или 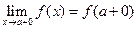
то точка 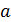 называется точкой разрыва первого рода.
называется точкой разрыва первого рода.
Пусть 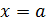 точка разрыва функции, не являющаяся точкой разрыва первого рода. Тогда ее называют точкой разрыва функции второго рода. В такой точке хотя бы один из односторонних пределов либо не существует, либо бесконечен.
точка разрыва функции, не являющаяся точкой разрыва первого рода. Тогда ее называют точкой разрыва функции второго рода. В такой точке хотя бы один из односторонних пределов либо не существует, либо бесконечен.
Например, для функции 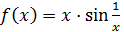 точка
точка 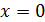 – точка разрыва первого рода. Доопределив эту функцию до непрерывности получим:
– точка разрыва первого рода. Доопределив эту функцию до непрерывности получим:
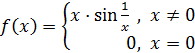 , непрерывную в точке
, непрерывную в точке 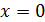 , так как
, так как 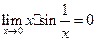 .
.
Для функций 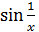 и
и 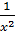 точка
точка 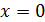 является точкой разрыва второго рода.
является точкой разрыва второго рода.
 2014-02-02
2014-02-02 925
925







