Теорема 4.2.1. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций.
Доказательство. Пусть у = u (x) ± v (x), где u = u (x) и v = v (x) – дифференцируемые функции. Поскольку D у = D u ± D v, то
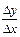 =
= 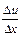 ±
± 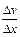 .
.
Тогда

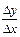 =
= 
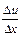 ±
± 
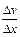 = u’ ± v’.
= u’ ± v’.
Следовательно,
(u ± v) ’ = u’ ± v’.
Теорема доказана.
Теорема 4.2.2. Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой:
(u × v)' = u' × v + u × v'.
Доказательство. Пусть у = u × v, где u = u (x) и v = v (x) – дифференцируемые функции. Так как D у = (u + D u)(v + D v) – u × v = u ×D v + v ×D u + D u ×D v, то 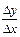 = u ×
= u ×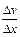 + v ×
+ v ×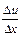 +
+ 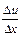 ×D v. Согласно теореме 4.1.1
×D v. Согласно теореме 4.1.1  D v = 0. Тогда получаем, что
D v = 0. Тогда получаем, что

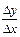 =
=  (u ×
(u ×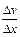 ) +
) +  (v ×
(v ×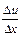 ) +
) +  (
(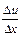 ×D v) =
×D v) =
u ×
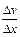 + v ×
+ v ×
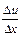 +
+ 
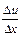 ×
× D v = u' × v + u × v' + u' ×0 = u' × v + u × v'.
D v = u' × v + u × v' + u' ×0 = u' × v + u × v'.
Теорема доказана.
Следствие. Постоянный множитель можно выносить за знак производной:
(с× v) ' = с× v'.
Теорема 4.2.3. Производная частного двух дифференцируемых функций определяется формулой
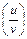 ¢ =
¢ = 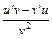 (v ¹ 0).
(v ¹ 0).
Доказательство. Если y = 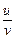 , где u = u (x) и v = v (x) – дифференцируемые функции, причём v (х) ¹ 0, то
, где u = u (x) и v = v (x) – дифференцируемые функции, причём v (х) ¹ 0, то
Dу = 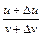 –
– 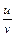 =
= 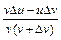 ,
,
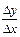 =
= 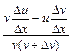 .
.
Следовательно,

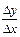 =
= 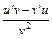 ,
,
так как  D v = 0. Теорема доказана.
D v = 0. Теорема доказана.
Если у = f (x) и х = j(у) – взаимно-обратные функции и у 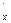 ¹ 0, то
¹ 0, то
х 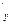 =
= 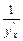 .
.
Действительно, так как 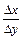 =
= 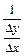 , то
, то
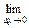
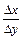 =
= 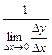 ,
,
откуда и следует, что х 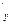 =
= 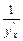 .
.
 2014-02-09
2014-02-09 672
672








