Индексы фиксированного состава

Чтобы исключить влияние изменения структуры совокупности на динамику средних величин, можно для двух периодов рассчитывать среднее по одной и той же структуре, которая, как правило, фиксируется по отчетному периоду. Индекс, показывающий динамику средних величин при одной и той же фиксированной структуре совокупности, носит название индекса фиксированного состава. Для индекса себестоимости это фиксирование одной и той же структуры найдет отражение в следующей формуле индекса:

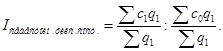
После сокращения на ∑q₁ этот индекс примет вид формулы агрегатного индекса:

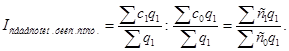
В этом индексе влияние структурного фактора устранено, поэтому он определяет средний размер изменения себестоимости на всех трех компаниях. Индекс фиксированного состава не может выходить за пределы значений частных индексов, ибо он является средним из них.

Чтобы убедиться в этом, рассчитаем индекс себестоимости фиксированного состава в нашем примере:

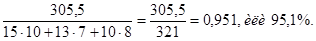
Этот индекс показывает, что в среднем по всем трем компаниям себестоимость снизилась на 4,9% (95,1 - 100,0). Так как индекс себестоимости переменного состава отражает на себе влияние двух факторов, а индекс фиксированного состава только усредняет изменение индексируемого показателя без учета изменения структуры совокупности, то представляется вполне логичным путем деления первого индекса на второй определить изменение среднего показателя за счет структурного фактора.

Относительную величину, получающуюся в результате деления индекса переменного состава на индекс фиксированного состава, можно условно назвать индексом структуры.

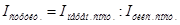
В нашем примере 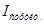= 0,912:0,951 = 0,96, или 96,0%. Это означает, что за счет изменения удельного веса отдельных компаний в общем выпуске продукции средняя себестоимость снизилась на 4% (96% - 100%). В частности, снижению средней себестоимости способствовало увеличение в общем выпуске удельного веса продукции компании «Дельта», у которой самая низкая себестоимость.

Чтобы лучше усвоить природу индексов переменного и фиксированного состава, применимых только для качественных показателей, рассмотрим пример, иллюстрирующий исчисление индексов урожайности переменного и фиксированного состава.

Пример. В табл. 10.6 приведены данные о посевных площадях и урожайности зерновых фермерских хозяйств Троицкого района.

Таблица 10.6