Квадратурные формулы Ньютона-Котеса

Если выбрать в качестве 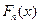интерполяционный многочлен Лагранжа 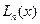с равноотстоящими узлами интерполяции, то полученные формулы численного интерполирования называют квадратными формулами Ньютона – Котеса.

Итак, имеем формулу численного интегрирования

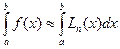(3)

Формула (3) будет формулой закрытого типа, если концы отрезка интегрирования являются узлами интерполяции и открытого типа, если хотя бы один из концов не является узлом интерполяции.

Запишем многочлен Лагранжа в краткой форме

,

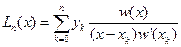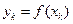
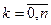
Тогда

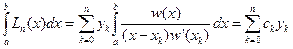
Где

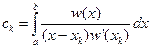
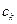не зависят от функции, а только от узлов интерполяции. Будем рассматривать равноотстоящие узлы с шагом h.

Многочлен Лагранжа для равноотстоящих узлов имеет вид:

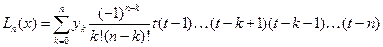
Где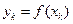

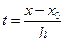
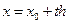
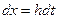
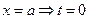
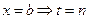
Для коэффициентов 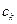окончательно получим:

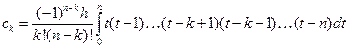(4)

Коэффициенты (4) и есть коэффициенты Котеса. Их можно подсчитать при различных т.

Пусть n=1. имеем 2 узла интерполяции и два коэффициента Котеса 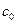и .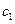

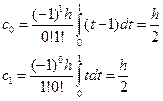
При n=2 имеем три узла коэффициента Котеса.

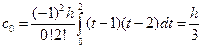
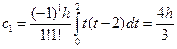
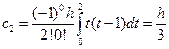
3. частные случаи численного интегрирования.

1) формула средних прямоугольников.

Подынтегральную функцию 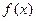заменим интерполяционным многочленом Лагранжа нулевой степени

,

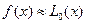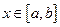
n=0, имеем один узел интерполяции, пусть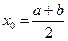

по условию интерполирования

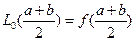
Тогда

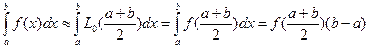(5)

Формула (5) и есть формула средних прямоугольников.

Геометрический смысл заключается в том, что площадь криволинейной трапеции заменяется на площадь прямоугольника.

y

f((a+b)/2)

a 0 (a+b)/2 b x

Замечание: можно получить ещё две формулы открытого типа. Если в качестве узла интерполирования выбрать 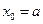или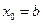

При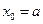

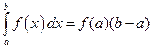- формула левых прямоугольников (5’)

При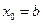

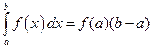- формула правых прямоугольников. (5’’)

Погрешность формулы средних прямоугольников.

Теорема: если функция 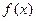имеет на 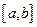непрерывные производные до второго порядка включительно, то

, ,

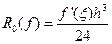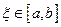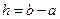
Доказательство

Так как функция 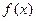имеет непрерывные производные до второго порялка, то по формуле Тейлора имеем:

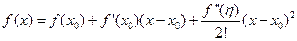
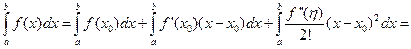
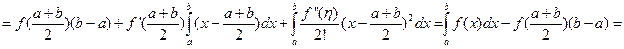
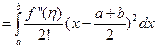
Правая часть дает погрешность метода. Применяя теорему о среднем значении интеграла, будем иметь:

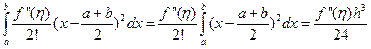
Теорема доказана.

Если найдется число 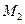, такое, что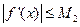 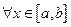, то получим оценку погрешности

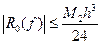
2) формула трапеций.

Подынтегральную функцию f(x) заменим интерполяционным многочленом Лагранжа первой степени.

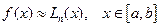
n=1, имеем два узла интерполирования. Выберем 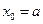и 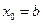. По формуле Ньютона – Котеса получим:

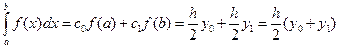(7)

Формула (7) и есть формула трапеции. Геометрический смысл формулы трапеций заключается в том, что за площадь криволинейной трапеции принимается площадь прямоугольной трапеции.

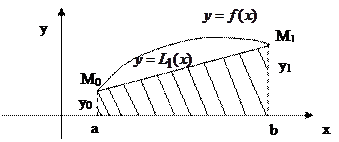Погрешность формулы трапеций.

При n=1 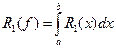, 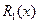- остаточный член формулы Лагранжа.

Теорема: если функция f(x) имеет непрерывные производные до второго порядка включительно, на отрезке 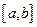, то погрешность

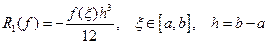
Доказательство:

Как и в предыдущем случае, применяя формулу Тейлора и, воспользовавшись теоремой о среднем значении интеграла, получим:

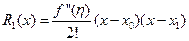
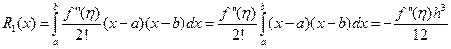
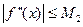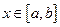Если для , то получим оценку погрешности метода:

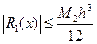(8)

3) формула парабол (Симпсона).

Подынтегральную функцию 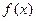заменим интерполяционным многочленом Лагранжа второй степени

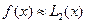
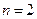, имеем три узла интерполяции. Выберем ,

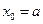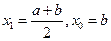
Узлы равноотстоящие, шаг 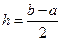. Имеем три коэффициента Котеса

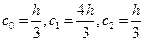
По формуле Ньютона – Котеса будем иметь:

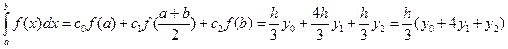(9)

Формула (9) и есть формула парабол (Симпсона).

Геометрический смысл заключается в том, что график функции 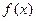заменяется графиком многочлена Лагранжа второй степени (параболой) на отрезке 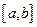. При вычислении интеграла по формуле (9)его численное значение будет равно площади криволинейной трапеции, ограниченной сверху дугой параболы, проходящей через точки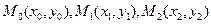

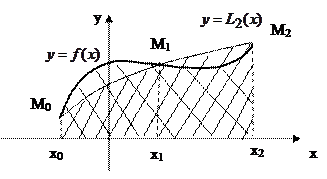Погрешность формулы парабол.

Теорема: если функция 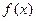имеет на отрезке 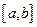непрерывные производные до четвертого порядка включительно, то погрешность формулы парабол можно вычислить по формуле:

, ,

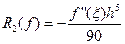
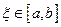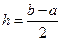Если для 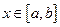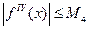, то получим оценку погрешности метода:

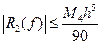(10)

Для увеличения точности при вычислении интеграла применяют следующий прием: отрезок интегрирования разбивают на достаточно большое число мельких промежутков и к каждому из частичных отрезков применяют квадратурную формулу Ньютона – Котеса с малым n. Получают формулы простой структуры, которые называют обобщенными формулами.

5. Обобщенные формулы численного интегрирования.

1) обобщенная формула средних прямоугольников.

Разделим отрезок интегрирования 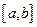на n равных частей, получим отрезки

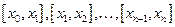
Шаг интегрирования 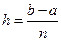. На каждом частичном отрезке применяем ранее полученную элементарную формулу средних прямоугольников и результаты складываем, таким образом, будем иметь обобщенную формулу средних прямоугольников.

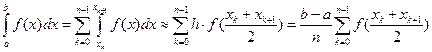(11)

Если за узел интерполирования на каждом частичном отрезке брать левый конец, то получим 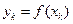, 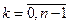и

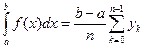- обобщенная формула левых прямоугольников (11a)

Если же за узлы выбирать правые концы, то 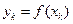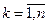и

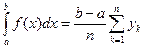- обобщенная формула правых прямоугольников (11в)

Погрешность обобщенной формулы средних прямоугольников.

На каждом частичном отрезке допускаемая погрешность вычисляется по формуле (6), имеем n частичных отрезков. Сложив погрешности, будем иметь:

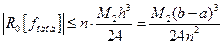(12)

Если удвоить число точек деления, то погрешность уменьшится в 4 раза.

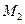- верхняя граница второй производной на отрезке .

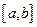2) обобщенная формула трапеций.

Отрезок интегрирования 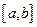разобьем на n равных частей точками 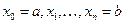, получим шаг интегрирования .

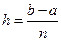На каждом частичном отрезке 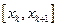применим элементарную формулу трапеций и полученные результаты просуммируем.

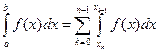
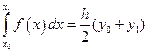
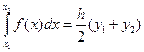
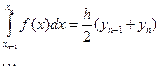
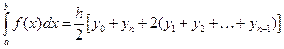(13)

Это и есть обобщенная формула трапеций.

Погрешность обобщенной формулы трапеций.

Допускаемая погрешность на каждом частичном отрезке вычисляется по формуле (10), тогда для всего отрезка 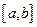получим:

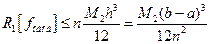(14)

Если удвоить число точек деления, то погрешность уменьшится в 4 раза.

3) обобщенная формула парабол.

Точность приближенного интегрирования заметно возрастает, если подынтегральную функцию 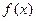на каждом частичном отрезок заменить квадратичной функцией. Разбиваем отрезок интегрирования 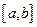на n равных частей, а затем каждый полученный отрезок делим еще пополам. В общем случае получили четное число 2n отрезков. Применим формулу (9) к каждой паре смежных отрезков разбиения.

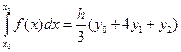
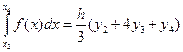
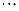
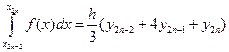
Суммируя равенства, получим обобщенную формулу парабол:

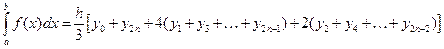(15)

Погрешность обобщенной формулы парабол.

На каждой паре смежных отрезков погрешность оценивается по формуле (10), имеем n пар, тогда

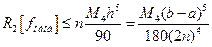(16)

На практике, если задача решается с использованием компьютера, погрешность вычисляется по формуле практической оценки погрешности, основанной на двойном просчете.

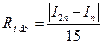, где

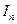- значение определенного интеграла, вычисленное при разбиении на n (n - четное).

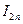- значение определенного интеграла, вычисленное при разбиении на 2n частей.