Закон больших чисел

Для практики очень важно знать такие усло­вия, чтобы предвидеть ход явлений. Эти условия и указываются в теоремах, носящих об­щее название закон больших чисел. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бер­нулли – простей­шим.

▲ Теорема 2.32. (Неравенство Чебышева). Вероятность того, что отклонение слу­чайной величины от ее математического ожидания по абсолютной величине м еньше положительного числа e не меньше, чем 1 – D (X)/e², т.е. P (| X – M (X)| <e) ³ 1 – D (X)/e².

▲ Теорема 2.33. (Теорема Чебышева). Если X ₁, X ₂, …, X_n попарно независимые слу­чайные величины, причем дис­персии их равномерно ограничены (не превышают по­сто­янного числа C), то как бы мало ни было положительное число e, вероятность не­равенства

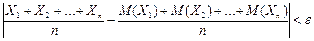
будет как угодно близка к единице, если число случайных величин достаточно ве­лико, т.е.

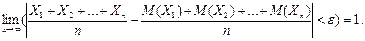
▲ Теорема 2.34. (Теорема Бернулли). При неограниченном уве­личении числа испыта­ний относительная частота W(A) события A сходится по вероятности к P (A) – вероят­ности его появления при одном испытании.

Пример 2.31. Игральный кубик бросали 3000 раз. Сколько раз выпала «шестерка»?

Решение. Точный ответ здесь, конечно, невозможен, а вот ска­зать, какого результата следует ожидать, можно. Вероятность выпадения «шестерки» равна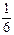, поэтому естественно ожидать, что частота должна быть близка к 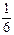. Пусть «шестерка» выпадет т раз, тогда 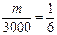, отсюда m≈ 500. Естественно ожидать, что «шестерка» выпадет около 500 раз.

Пример 2.32. Для того, чтобы оценить число рыб в пруду посту­пают следующим образом. Сетью ловят, скажем, 200 рыб, ставят на них метки и обратно отпускают в пруд. Через некоторое время снова ловят 200 рыб. Пусть среди них всего четыре рыбы окажутся поме­ченными. 200 рыб состав­ляют случайную выборку. Раз на каждые 200 рыб приходятся четыре помеченных, то 200 помечен­ных рыб прихо­дятся примерно на 10 000, т.е. в пруду приблизительно 10 000 рыб.