Деформация – изменение объема или формы твердого тела без изменения его массы под действием внешней силы. Деформация – это процесс, при котором изменяется расстояние между какими-либо точками тела. Простейшие виды деформации: растяжение, сжатие, сдвиг, кручение, изгиб.
Элементарной деформацией при одноосном растяжении цилиндрического образца является удлинение. При приложении растягивающей силы образец увеличивается в длине и уменьшается в диаметре. Обычно деформацию выражают в относительных единицах. Так, если образец имел начальную длину l0 и lk после приложения растягивающей силы (рисунок 6.3), то относительная деформация образца
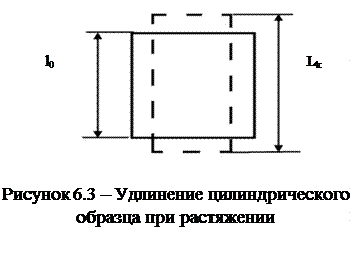 |
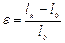 .
. Для полного описания деформированного состояния кроме удлинений (укорочений) необходимо знать сдвиги, возникающие под действием касательных напряжений. При механических испытаниях принято характеризовать деформации относительным изменением линейных размеров образцов, а также углом сдвига, т. е. углом, на который изменился первоначальный прямой угол элемента поверхности деформируемого тела или образца. Относительным сдвигом называют тангенс угла сдвига (рисунок 6.4):
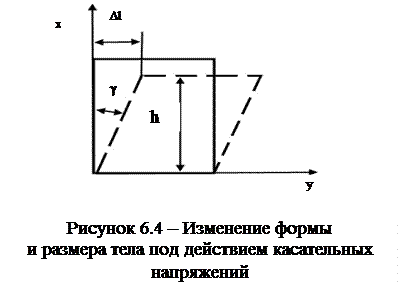 |
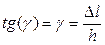 .
.
Любая деформация может быть представлена в виде определенной комбинации сдвигов и удлинений. В общем случае деформированное состояние в выбранной точке характеризуется девятью величинами εij, которые являются компонентами тензора второго ранга – тензора деформаций:
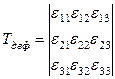 .
.
Рассматривая случай объемной деформации твердого тела, выберем в качестве осей координат три ортогональные оси х, у, z с началом в точке О (рисунок 6.5). Пусть точка О после деформации осталась на месте, а все остальные точки тела изменили свои положения. Определим положение точки А (х, у, z) до деформации радиус-вектором  . После деформации точка А (х, у, z) переместится в положение А ' (х ', у ', z '), определяемое радиусом-вектором
. После деформации точка А (х, у, z) переместится в положение А ' (х ', у ', z '), определяемое радиусом-вектором 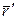 . Вектор
. Вектор 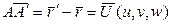 называется вектором смещения,
называется вектором смещения, 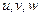 – компоненты вектора смещения по осям x, y, z.
– компоненты вектора смещения по осям x, y, z.
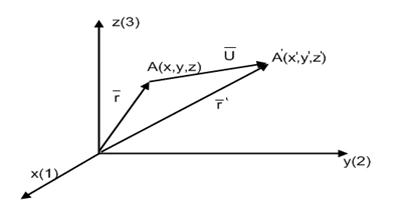
Рисунок 6.5 – Координатные оси для описания
упруго деформированного состояния
Компоненты вектора смещения связаны с компонентами тензора деформаций соотношениями Коши:
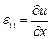 ,
, 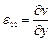 ,
, 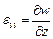 ,
,
 ,
,
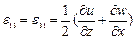 ,
,
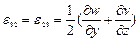 .
.
Компоненты 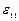 ,
, 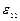 ,
, 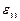 задают относительное удлинение вдоль соответствующих осей, а компоненты
задают относительное удлинение вдоль соответствующих осей, а компоненты 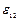 ,
, 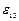 ,
,  задают изменения углов, вызванные приложением нагрузки.
задают изменения углов, вызванные приложением нагрузки.
 2014-02-09
2014-02-09 1146
1146
