9.4.1. Однопериодная модель со случайным спросом. Поскольку на поступление продуктов, спрос на них, на время выполнения заказов оказывает влияние множество случайных факторов, вызывая их колебания, то эти величины являются случайными величинами. Так как определяющим фактором в моделях является спрос, то рассмотрим модели со случайным спросом.
Будем предполагать, что спрос на продукцию или расход материальных ресурсов является стационарной случайной величиной с математическим ожиданием 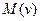 и конечной дисперсией
и конечной дисперсией 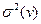 . Рассмотрим случай, когда спрос v –дискретная случайная величина, заданна рядом распределения:
. Рассмотрим случай, когда спрос v –дискретная случайная величина, заданна рядом распределения:
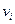 | … | k | … | |||
p(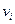 ) ) | p(0) | p(1) | p(2) | … | p(k) | … |
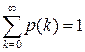 . Числовые характеристики этой случайной величины вычисляются по формулам:
. Числовые характеристики этой случайной величины вычисляются по формулам:
- дисперсия:  ;
;
- вероятность того, что спрос 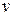 не превысит величины
не превысит величины 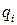 - это сумма вероятностей:
- это сумма вероятностей: 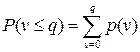 .
.
Партия поставки продукции или партия запуска продукции в производство вычисляется при следующих предположениях:
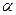 - покупная цена (или стоимость) единицы продукции;
- покупная цена (или стоимость) единицы продукции;
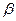 (
(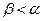 ) - цена реализации неиспользованной продукции;
) - цена реализации неиспользованной продукции;
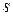 - затраты на содержание единицы продукции в единицу времени;
- затраты на содержание единицы продукции в единицу времени;
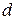 - издержки, связанные с дефицитом продукции.
- издержки, связанные с дефицитом продукции.
Функция издержек при случайном спросе определяется математическим ожиданием издержек функционирования системы и состоит из: издержек приобретения заказа, содержания запаса, дефицита, реализации неиспользованной продукции.
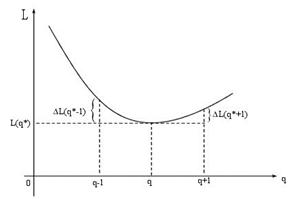
Рис. 9.12
Поскольку функция издержек 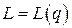 системы унимодальная (см. рис. 9.12), то оптимальной считаем такую величину заказа
системы унимодальная (см. рис. 9.12), то оптимальной считаем такую величину заказа  , при которой математическое ожидание издержек функционирования системы минимально, т. е. должны выполняться нервенства:
, при которой математическое ожидание издержек функционирования системы минимально, т. е. должны выполняться нервенства:
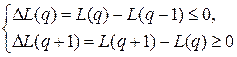 (9.20)
(9.20)
где 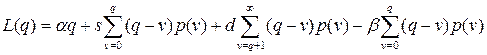 .
.
Так как 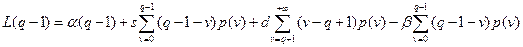 и
и
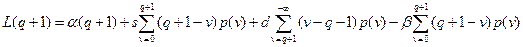 , то подставив эти значения в систему (9.20), получим:
, то подставив эти значения в систему (9.20), получим:
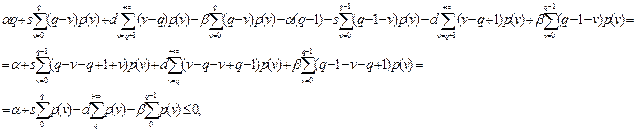
или
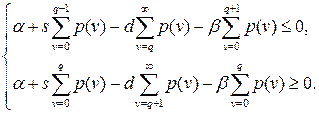
Так как 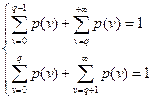 , то подставляя
, то подставляя 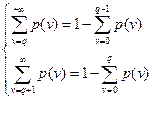 , получим систему:
, получим систему:
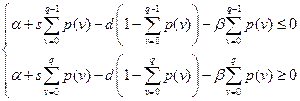 ,
,
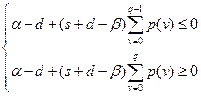 ,
,
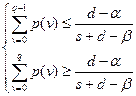 или
или 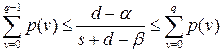 .
.
Из последней системы следует неравенство для нахождения оптимальной партии поставки
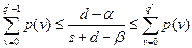 или
или 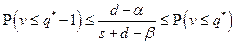 (9.21)
(9.21)
Среднее количество неиспользованной продукции равно математическому ожиданию спроса, не превышающего оптимальные значения q*: 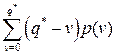 .
.
Минимальные издержки функционирования системы в единицу времени составляют
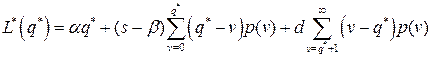 .
.
Пример 9.9. Предприятие производит продукцию, спрос на которую в течение года задан рядом распределения:
| Спрос v, тыс. шт. | ||||||
| Вероятность спроса, p(v) | 0,1 | 0,15 | 0,1 | 0,2 | 0,25 | 0,2 |
Стоимость изготовления 1000 единиц продукции равна 150 ден. ед. Издержки из-за дефицита единицы продукции составляю 0,2 ден. ед. Неиспользованная продукция в конце года реализуется по цене 50 ден. ед. за 1000. Издержки содержания составляют 10% первоначальной стоимости. Определить оптимальную партию производства продукции, среднее число неиспользованной продукции и издержки, связанные с производством, хранением и дефицитом продукции.
Решение. Спрос V на продукцию является дискретной случайной величиной. В условии задачи заданны: стоимость изготовления 1000 ед. продукции 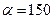 ден. ед.; издержки дефицита одной единицы продукции d=0,2 ден. ед., а 1000 ед. продукции –
ден. ед.; издержки дефицита одной единицы продукции d=0,2 ден. ед., а 1000 ед. продукции – 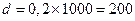 ден. ед.; издержки содержания 1000 ед. продукции составляет
ден. ед.; издержки содержания 1000 ед. продукции составляет 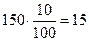 ден. ед. Нереализованная продукция в конце года распродается по 50 ден. ед. Для того, чтобы найти оптимальную партию производства продукции воспользуемся неравенством (9.21), предварительно определив накопленные вероятности спроса:
ден. ед. Нереализованная продукция в конце года распродается по 50 ден. ед. Для того, чтобы найти оптимальную партию производства продукции воспользуемся неравенством (9.21), предварительно определив накопленные вероятности спроса:
| Спрос, v, тыс. шт. | ||||||
Накопленные вероятности, 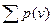 | 0,1 | 0,25 | 0,35 | 0,55 | 0,8 | 1,0 |
Вычислим величину 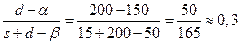 .
.
Следовательно, оптимальная партия производства продукции должена удовлетворять неравенству:
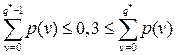 .
.
Значение 0,3 находится между накопленными вероятностями 0,25 и 0,35, которым соответствуют значения спроса 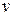 = 15 и
= 15 и 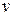 = 20. Значит, оптимальное значение
= 20. Значит, оптимальное значение 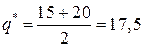 тыс. ед. продукции.
тыс. ед. продукции.
Среднее количество неиспользованной продукции будет равно:
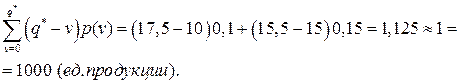
Минимальные издержки работы системы составят:
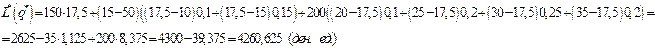
9.4.2. Модель при наличии страхового запаса. Предположим,что спрос 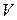 на продукцию является стационарной случайной величиной с математическим ожиданием
на продукцию является стационарной случайной величиной с математическим ожиданием 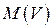 и конечной дисперсией
и конечной дисперсией 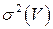 . Для бесперебойной работы, при случайных колебаниях спроса, предприятию необходим некоторый запас продукции, который называют страховым запасом и обозначают
. Для бесперебойной работы, при случайных колебаниях спроса, предприятию необходим некоторый запас продукции, который называют страховым запасом и обозначают 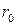 . Вероятность того, что спрос не превысит величины
. Вероятность того, что спрос не превысит величины 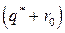 , называют коэффициентом надежности и обозначают
, называют коэффициентом надежности и обозначают 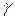 . Как правило, коэффициент надежности
. Как правило, коэффициент надежности 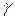 равен 0,9; 0,95 или 0,99. Вероятность противоположного события, состоящего в том, что спрос превысит величину
равен 0,9; 0,95 или 0,99. Вероятность противоположного события, состоящего в том, что спрос превысит величину 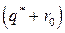 , называют коэффициентом риска
, называют коэффициентом риска 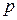 , т. е.
, т. е. 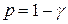 . Если известна плотность распределения вероятностей
. Если известна плотность распределения вероятностей 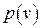 спроса
спроса 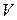 , то коэффициент надежности можно вычислить по формуле:
, то коэффициент надежности можно вычислить по формуле:
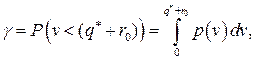
а коэффициент риска по формуле:
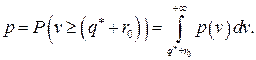
Зная закон распределения спроса и коэффициент надежности, оптимальный страховой запас можно найти из равенства:
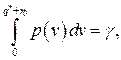 (9.22)
(9.22)
воспользовавшись соответствующей таблицей закона распределения.
При наличии страхового запаса 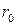 издержки работы системы в единицу времени описываются функцией
издержки работы системы в единицу времени описываются функцией
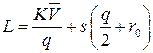 ,
,
где 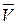 - средняя арифметическая спроса. Вычислив производную
- средняя арифметическая спроса. Вычислив производную 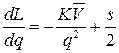 , приравняв ее нулю, находим минимальный объем партии поставки:
, приравняв ее нулю, находим минимальный объем партии поставки: 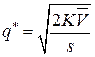 .
.
Тогда минимальные издержки составят: 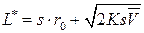 .
.
Рассмотрим, как определяется страховой запас, в зависимости от закона распределения спроса.
1. Пусть спрос на продукцию подчиняется нормальному закону распределения. Функция плотности распределения вероятностей нормального закона имеет вид
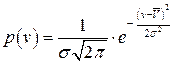 ,
,
где 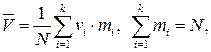 - средняя арифметическая спроса, которая является оценкой математического ожидания;
- средняя арифметическая спроса, которая является оценкой математического ожидания; 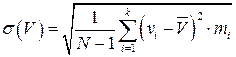 - среднее статистическое квадратическое отклонение спроса;
- среднее статистическое квадратическое отклонение спроса;  - частота, с которой встречается величина спроса
- частота, с которой встречается величина спроса 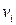 ;
; 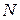 - количество наблюдений.
- количество наблюдений.
Выполнив замену 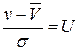 в функции
в функции 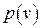 и воспользовавшись центральной предельной теоремой, преобразуем плотность нормального закона к виду
и воспользовавшись центральной предельной теоремой, преобразуем плотность нормального закона к виду 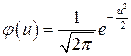 . Функция
. Функция 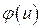 - это плотность распределения центрированной и нормированной случайной величины, имеющей нормальное распределение. Для того чтобы найти оптимальный страховой запас при нормальном законе распределения нужно по заданному коэффициенту риска
- это плотность распределения центрированной и нормированной случайной величины, имеющей нормальное распределение. Для того чтобы найти оптимальный страховой запас при нормальном законе распределения нужно по заданному коэффициенту риска 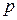 (или по коэффициенту надежности
(или по коэффициенту надежности 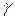 ) найти значение центрированной и нормированной случайной величины
) найти значение центрированной и нормированной случайной величины 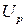 (
(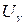 ) из равенств
) из равенств
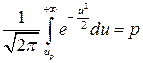 или
или 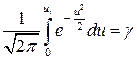 .
.
Поскольку 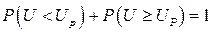 , то
, то 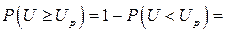
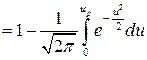 , где
, где 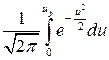 - функция Лапласа. Зная коэффициент риска
- функция Лапласа. Зная коэффициент риска 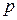 (или коэффициент надежности
(или коэффициент надежности 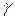 ), по таблице функции Лапласа находим
), по таблице функции Лапласа находим 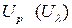 . Страховой запас определяется таким образом, чтобы случайный спрос, не превосходил суммы среднего значения спроса и страхового запаса
. Страховой запас определяется таким образом, чтобы случайный спрос, не превосходил суммы среднего значения спроса и страхового запаса 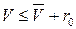 с вероятностью
с вероятностью 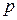 , т. е.
, т. е. 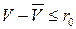 . Учитывая, что
. Учитывая, что 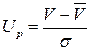 , получим формулу для определения страхового запаса при нормальном законе распределения:
, получим формулу для определения страхового запаса при нормальном законе распределения: 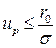
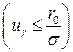 или
или 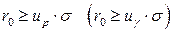 . Из этого неравенства находим минимальное значение страхового запаса:
. Из этого неравенства находим минимальное значение страхового запаса: 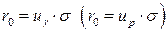 . Минимальные издержки при нормальном законе распределения определяются по формуле:
. Минимальные издержки при нормальном законе распределения определяются по формуле:
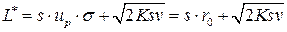 .
.
2. Пусть спрос описывается показательным законом распределения с плотностью распределения вероятностей
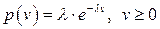 .
.
Оптимальный страховой запас находим из равенства
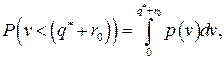 т. е.
т. е. 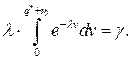
Поскольку оценка параметра 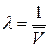 , то получим равенство
, то получим равенство 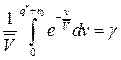 , из которого последовательно находим:
, из которого последовательно находим:
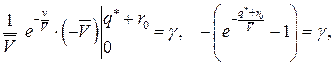
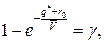
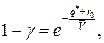
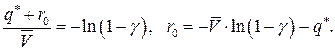
Пример 9.10. На кондитерской фабрике для упаковки готовой продукции используется упаковочная бумага. Затраты на организацию заказа составляют 50 ден.ед. Ежедневная потребность в упаковочной бумаге в течение года приведена в таблице
Потребность в упаковочной бумаге, 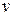 , кг , кг | [0,100) | [100,200) | [200,300) | [300,400) | [400,500) | [500,600) | [600,700) | [700,800) | [800,900) | [900,1000) |
Частота,  |
Определить величину страхового запаса упаковочной бумаги, гарантирующего бесперебойное снабжение с надежностью 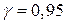 и минимальные издержки обеспечения упаковочной бумагой в течение года при наличии страхового запаса, если стоимость хранения 1кг упаковочной бумаги составляет 10 ден. ед. в год.
и минимальные издержки обеспечения упаковочной бумагой в течение года при наличии страхового запаса, если стоимость хранения 1кг упаковочной бумаги составляет 10 ден. ед. в год.
Решение. Вначале определим закон распределения спроса на упаковочную бумагу. Для этого построим гистограмму. На оси О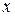 отложим интервалы спроса и на каждом интервале построим прямоугольник, площадь которого равна относительной частоте спроса (рис. 9.13).
отложим интервалы спроса и на каждом интервале построим прямоугольник, площадь которого равна относительной частоте спроса (рис. 9.13).

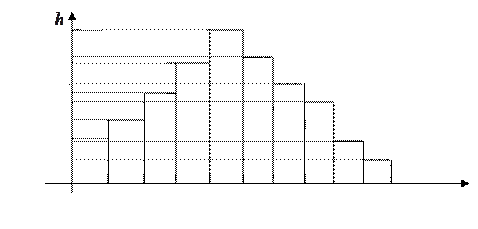
Рис.9.13
По виду гистограммы можно сделать предположение о нормальном законе распределении спроса на упаковочную бумагу. Проверим гипотезу о том, что распределение спроса на упаковочную бумагу подчиняется нормальному закону распределения по следующей схеме.
1. Сформулируем основную гипотезу 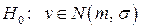 - спрос подчиняется нормальному закону распределения и альтернативную гипотезу
- спрос подчиняется нормальному закону распределения и альтернативную гипотезу 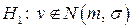 - спрос не подчиняется нормальному закону распределения.
- спрос не подчиняется нормальному закону распределения.
2. Зададим уровень значимости 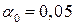 .
.
3. Объем выборки задан 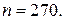
4. Для проверки гипотезы 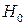 воспользуемся критерием хи - квадрат:
воспользуемся критерием хи - квадрат: 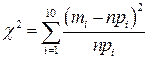 .
.
По таблице критических значений 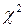 - распределения по уровню значимости
- распределения по уровню значимости 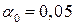 и числу степеней свободы
и числу степеней свободы 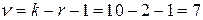 находим квантиль
находим квантиль 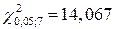 . Тогда интервал
. Тогда интервал 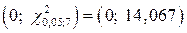 определяет область принятия гипотезы, а полуинтервал
определяет область принятия гипотезы, а полуинтервал 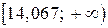 - критическая область.
- критическая область.
5. Вычислим числовые характеристики выборки 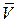 и
и 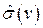 , которые являются оценками математического ожидания
, которые являются оценками математического ожидания 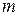 и среднего квадратического отклонения
и среднего квадратического отклонения 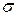 нормального закона распределения. Среднее арифметическое равно:
нормального закона распределения. Среднее арифметическое равно:
6.
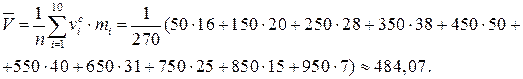
Среднее статистическое квадратическое отклонение:
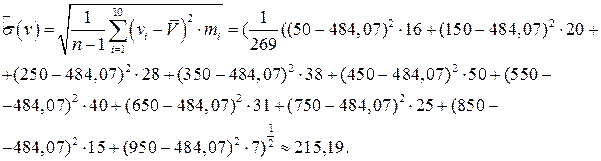

Тогда функция нормального закона распределения будет иметь вид:
 . Теоретические частоты вычислим по формуле:
. Теоретические частоты вычислим по формуле:
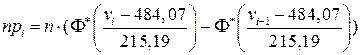 , при этом наименьшее значение
, при этом наименьшее значение
дроби 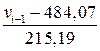 заменяем на «
заменяем на «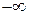 », а наибольшее – на «
», а наибольшее – на «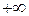 ».
».
 =270(0,0375-0)= =10,125; и т. д.
=270(0,0375-0)= =10,125; и т. д.
Вычисление значения 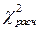 по эмпирическим данным сведем в таблицу 9.5.
по эмпирическим данным сведем в таблицу 9.5.
Таблица 9.5
Потребность в упаковочной бумаге, 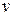 (кг) (кг) 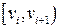 | Частоты,  | 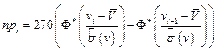 | 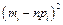 |  |
 [0;100) [0;100) | 10,125 | 34,516 | 3,4430 | |
| [100; 200) | 15,093 | 24,0787 | 1,5952 | |
| [200; 300) | 27,405 | 0,3540 | 0,0129 | |
| [300; 400) | 41,418 | 11,6824 | 0,2821 | |
| [400; 500) | 48,492 | 2,2741 | 0,0469 | |
| [500; 600) | 47,925 | 62,8056 | 1,3105 | |
| [600; 700) | 36,693 | 32,4103 | 0,8833 | |
| [700; 800) | 23,733 | 1,6053 | 0,0676 | |
| [800; 900) | 12,042 | 8,7498 | 0,7266 | |
| [900; 1000] | 7,074 | 0,0055 | 0,0008 | |
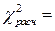 8,3689 8,3689 |
По таблице критических значений 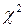 - распределения по уровню значимости
- распределения по уровню значимости  и числу степеней свободы
и числу степеней свободы 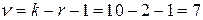 находим
находим 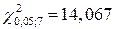 . Так как
. Так как 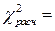 8,3689 меньше
8,3689 меньше 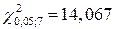 , то оснований для отклонения нулевой гипотезы
, то оснований для отклонения нулевой гипотезы 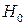 нет.
нет.
Итак, спрос на упаковочную бумагу подчиняется нормальному закону распределения, и страховой запас определим по формуле: 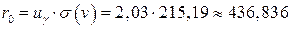 , где
, где 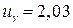 находим по таблице значений функции
находим по таблице значений функции 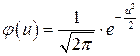 . Минимальные издержки при наличии страхового запаса равны:
. Минимальные издержки при наличии страхового запаса равны:
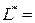
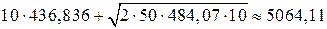 (ден.ед.)
(ден.ед.)
 2014-02-09
2014-02-09 4639
4639

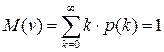 ;
;






