9.2.1. Простейшая модель оптимального размера партии поставки (модель Уилсона). Модель Уилсона основана на выборе такого фиксированного размера заказываемой партии, которая минимизирует расходы на заказываемый объем и содержание ресурса. Модель оптимальной партии поставки строится при следующих предположениях:
- уровень запаса снижается равномерно в соответствии с равномерно поступающими требованиями – спросом n.
- заказ выполняется мгновенно, т.е. время доставки равно нулю и уровень запаса восстанавливается до значения равного  .
.
- накладные расходы, связанные с размещением заказа и поставкой партии, не зависят от объема партии  и равны постоянной величине
и равны постоянной величине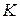 ;
;
- издержки содержания единицы продукции в единицу времени равны 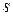 .
.
Динамика изменения уровня запаса 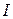 в модели Уилсона представленная на рис. 9.1. определяется следующим образом. Предположим, что в начальный момент времен уровень запаса
в модели Уилсона представленная на рис. 9.1. определяется следующим образом. Предположим, что в начальный момент времен уровень запаса 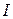 равен
равен  . Затем в течение времени
. Затем в течение времени 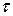 уровень запаса равномерно снижается до 0, после чего подается заказ на доставку новой партии объема
уровень запаса равномерно снижается до 0, после чего подается заказ на доставку новой партии объема  . Заказ выполняется мгновенно и уровень запаса восстанавливается до величины
. Заказ выполняется мгновенно и уровень запаса восстанавливается до величины  .
.
|
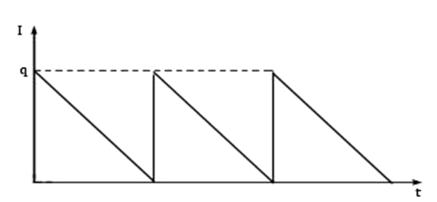
Рис. 9.1
Интервал времени длиной 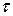 между поставками называется циклом. Очевидно, что
между поставками называется циклом. Очевидно, что 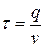 .
.
Затраты 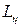 в течение цикла
в течение цикла 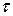 состоят из накладных расходов
состоят из накладных расходов 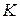 и издержек содержания запаса, которые пропорциональны средней величине текущего запаса
и издержек содержания запаса, которые пропорциональны средней величине текущего запаса 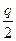 и времени содержания (длине цикла)
и времени содержания (длине цикла) 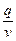 :
:

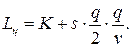
Разделив это выражение на длину цикла 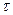 , получим издержки в единицу времени:
, получим издержки в единицу времени:
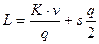 . (9.1)
. (9.1)
Издержки в единицу времени 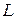 являются функцией переменной
являются функцией переменной  . Поскольку издержки
. Поскольку издержки 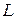 должны быть минимальными, то найдем минимум функции
должны быть минимальными, то найдем минимум функции 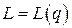 . Для этого вычислим производную первого порядка и приравняем ее к нулю. Последовательно выполняя преобразования найдем стационарную точку.
. Для этого вычислим производную первого порядка и приравняем ее к нулю. Последовательно выполняя преобразования найдем стационарную точку.
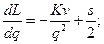
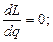
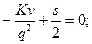
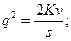
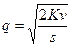 .
.
Так как 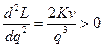 для всех
для всех  > 0, то
> 0, то
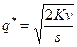 (9.2)
(9.2)
точка минимума функции 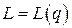 . Следовательно, если объем партии равен
. Следовательно, если объем партии равен 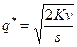 , то издержки (9.1) при этом значении
, то издержки (9.1) при этом значении 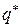 достигают минимального значения. Формулу (9.2) называют формулой размера партии, экономичной величиной заказа, формулой квадратного корня или формулой Уилсона. Зная минимальный размер партии
достигают минимального значения. Формулу (9.2) называют формулой размера партии, экономичной величиной заказа, формулой квадратного корня или формулой Уилсона. Зная минимальный размер партии 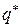 , вычислим:
, вычислим:
- минимальный интервал между поставками
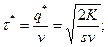
- минимальный средний уровень текущего запаса
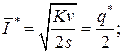
- минимальные затраты по формированию заказа и содержанию запасов в единицу времени
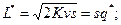
- минимальное число поставок за период 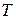
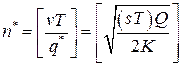 или
или 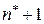 ,
,
где 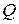 =
= 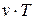 – потребление за период
– потребление за период 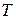 ,
, 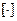 - наибольшее целое число, не превосходящее данное.
- наибольшее целое число, не превосходящее данное.
Если ввести в рассмотрение издержки размещения заказа в единицу времени 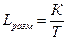 и средние издержки содержания запаса
и средние издержки содержания запаса 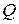 в единицу времени
в единицу времени 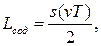 то минимальные затраты равны удвоенному среднему геометрическому из издержек размещения и содержания запаса:
то минимальные затраты равны удвоенному среднему геометрическому из издержек размещения и содержания запаса: 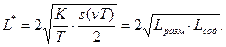
Если задана не интенсивность потребления 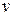 в единицу времени, а общий его объем запаса Q за период Т, то
в единицу времени, а общий его объем запаса Q за период Т, то 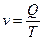 и тогда параметры модели Уилсона будут вычисляться по формулам:
и тогда параметры модели Уилсона будут вычисляться по формулам:
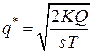 ,
, 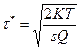 ,
, 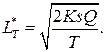
Модель Уилсона может быть использована при расчете оптимальной партии запуска продукции в производство. В этом случае величины, входящие в модель имеют другой смысл:
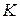 - издержки, связанные с переналадкой оборудования, не зависящие от величины выпускаемой партии;
- издержки, связанные с переналадкой оборудования, не зависящие от величины выпускаемой партии;
 – величина партии запуска;
– величина партии запуска;
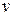 - интенсивность потребления (например, годовая потребность в продукции);
- интенсивность потребления (например, годовая потребность в продукции);
s - издержки содержания единицы продукции в единицу времени. Издержки содержания при вычислении оптимальной партии запуска могут определяться величиной процента от стоимости единицы продукции 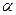 , т.е.
, т.е. 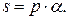 Параметры модели Уилсона выпуска продукции партиями будут вычисляться по формулам:
Параметры модели Уилсона выпуска продукции партиями будут вычисляться по формулам:
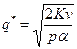 ;
; 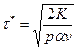 ;
; 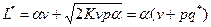 .
.
9.2.2. Свойства модели Уилсона. Рассмотрим некоторые свойства модели Уилсона:
1. При стационарном детерминированном спросе оптимальная партия поставки достигается при равенстве издержек формирования запаса и издержек их содержания, т.е.
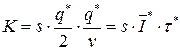 .
.
Это равенство получаем из уравнения 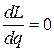 , т.е.
, т.е. 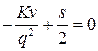 , которое разрешаем относительно
, которое разрешаем относительно 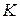 .
.
2. Величина партии поставки пропорциональна корню квадратному из интенсивности потребления, т.е.
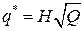 ,
, 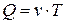 ,
, 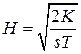 .
.
Эта формула применяется для приближенного расчета партии поставки. Вместо вычисления издержек 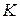 и
и 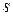 , что очень сложно, находят величину
, что очень сложно, находят величину 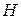 . Величина
. Величина 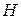 определяется из статистической отчетности, применяя корреляционно-регрессионный анализ.
определяется из статистической отчетности, применяя корреляционно-регрессионный анализ.
3. Централизуя запас 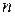 потребностей, общий уровень текущего запаса можно снизить в
потребностей, общий уровень текущего запаса можно снизить в 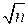 раз.
раз.
4. С ростом величины потребления должны расти абсолютные запасы. Из неравенства 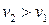 следует неравенство:
следует неравенство: 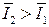 , но
, но 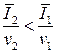 , т.е. темпы роста потребностей должны опережать темпы роста запасов (с ростом потребностей должны увеличиваться абсолютные запасы, а относительные уменьшаться).
, т.е. темпы роста потребностей должны опережать темпы роста запасов (с ростом потребностей должны увеличиваться абсолютные запасы, а относительные уменьшаться).
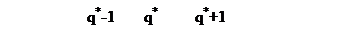
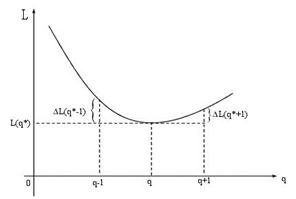
График функции L=L(q)
9.2.3. Учет точки заказа. При построении модели Уилсона предполагалось, что заказы выполняются мгновенно. В действительности необходимо учитывать время их доставки. Пусть 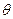 время от момента размещения заказа до момента его появления у потребителя. Чтобы избежать дефицита, заказ должен подаваться в тот момент, когда в запасе еще имеется наличный ресурс, количество которого должно быть достаточно для удовлетворения потребности на время выполнения заказа. Величину наличного запаса, при котором подается заказ на пополнение, будем называть точкой возобновления заказа и обозначать
время от момента размещения заказа до момента его появления у потребителя. Чтобы избежать дефицита, заказ должен подаваться в тот момент, когда в запасе еще имеется наличный ресурс, количество которого должно быть достаточно для удовлетворения потребности на время выполнения заказа. Величину наличного запаса, при котором подается заказ на пополнение, будем называть точкой возобновления заказа и обозначать 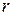 . Пусть
. Пусть 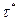 - минимальный интервал между поставками (длина цикла), то при определении точки возобновления заказа рассматривается 3 случая:
- минимальный интервал между поставками (длина цикла), то при определении точки возобновления заказа рассматривается 3 случая:
а) 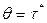 , б)
, б) 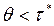 , в)
, в) 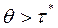 .
.
а) Если 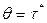 , то в момент поступления очередной партии следует подавать заказ на следующую очередную партию. Точка заказа при
, то в момент поступления очередной партии следует подавать заказ на следующую очередную партию. Точка заказа при 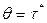 равна нулю:
равна нулю: 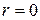 . Сумма наличного запаса и заказного ресурса в любой момент времени называется фиктивным уровнем
. Сумма наличного запаса и заказного ресурса в любой момент времени называется фиктивным уровнем 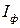 текущего запаса. При
текущего запаса. При 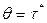 средний уровень фиктивного запаса равен:
средний уровень фиктивного запаса равен: 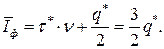 Динамика изменения текущего уровня фиктивности запаса при
Динамика изменения текущего уровня фиктивности запаса при 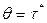 показана на рис. 9.2 пунктирной линией. От момента размещения заказа до момента прибытия заказа невыполненных заказов нет. Фиктивный уровень запаса совпадает с наличным.
показана на рис. 9.2 пунктирной линией. От момента размещения заказа до момента прибытия заказа невыполненных заказов нет. Фиктивный уровень запаса совпадает с наличным.
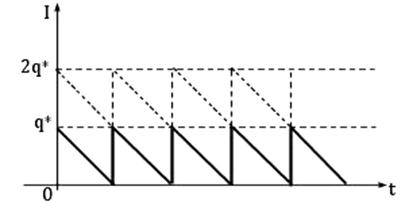
Рис. 9.2
Средний уровень фиктивности запаса равен 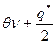 .
.
б) Если 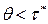 (время выполнения заказа меньше длины одного цикла), то точка размещения заказа
(время выполнения заказа меньше длины одного цикла), то точка размещения заказа 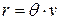 . Средний уровень фиктивности запаса равен:
. Средний уровень фиктивности запаса равен: 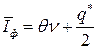 . Динамика изменения фиктивного уровня запаса при
. Динамика изменения фиктивного уровня запаса при 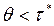 показана на рис. 9.3., где
показана на рис. 9.3., где 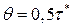 . От момента размещения заказа до момента прибытия заказа невыполненных заказов нет.
. От момента размещения заказа до момента прибытия заказа невыполненных заказов нет.
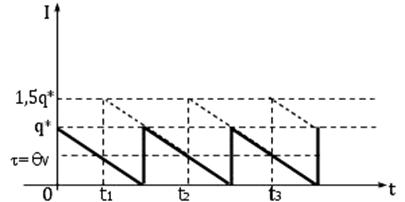
Рис. 9.3.
в) Если 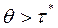 , то точка размещения заказа вычисляется по формуле:
, то точка размещения заказа вычисляется по формуле:
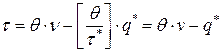 , где
, где 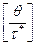 - целая часть числа
- целая часть числа 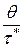 . Динамика изменения фиктивного уровня запаса при
. Динамика изменения фиктивного уровня запаса при 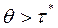 , приведена на рис. 9.4., где
, приведена на рис. 9.4., где 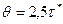 .
.
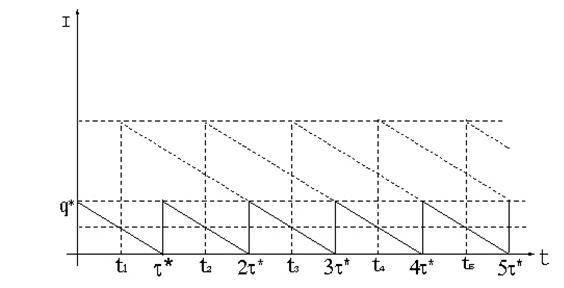
Рис. 9.4
Для бездефицитной работы в системе в начальный момент времени необходим некоторый начальный запас 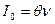 . Чтобы заказанная партия была доставлена не позже полного расходования начального запаса, заказ нужно разместить в момент времени
. Чтобы заказанная партия была доставлена не позже полного расходования начального запаса, заказ нужно разместить в момент времени 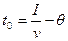 , где
, где 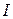 – фактический наличный начальный запас. Для бездефицитной работы величина фактического наличного начального запаса
– фактический наличный начальный запас. Для бездефицитной работы величина фактического наличного начального запаса 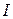 должна быть больше
должна быть больше 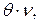 где
где 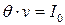 . Тогда
. Тогда 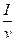 - время потребления фактического наличного начального запаса. Остальные заказы должны быть размещены в момент времени:
- время потребления фактического наличного начального запаса. Остальные заказы должны быть размещены в момент времени:
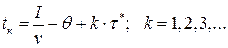
Пример 9.1. Предположим, что средняя потребность предприятия в сырье составляет 9 тыс. тонн в год. Издержки размещения заказа - 20 ден. ед., содержание одной тонны – 4 ден. ед. в год. Среднее время реализации заказа – 15 дней. Определить оптимальную партию поставки, периодичность возобновления заказа, точку размещения заказа, минимальный наличный запас сырья, моменты повторения заказов, минимальные издержки на размещение заказов и их содержание. Построить график динамики изменения фиктивного уровня запаса.
Решение. В задаче заданы величины: 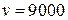 тонн в год;
тонн в год; 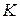 = 20 ден.ед.;
= 20 ден.ед.; 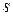 = 4 ден.ед.;
= 4 ден.ед.; 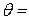 15 дней =
15 дней = 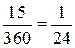 года = 0,042 года. Поскольку не определены условия доставки сырья, то считаем, что заказанная партия доставляется мгновенно. Следовательно, для определения оптимальных параметров работы предприятия применим модель Уилсона. Минимальную партию поставки сырья находим по формуле Уилсона:
года = 0,042 года. Поскольку не определены условия доставки сырья, то считаем, что заказанная партия доставляется мгновенно. Следовательно, для определения оптимальных параметров работы предприятия применим модель Уилсона. Минимальную партию поставки сырья находим по формуле Уилсона:
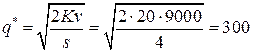 (тонн).
(тонн).
Минимальный интервал возобновления поставки заказа:
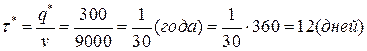 .
.
Так как точка размещения заказа 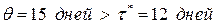 , то точка размещения заказа, равна:
, то точка размещения заказа, равна:
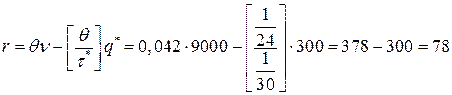 (тонн).
(тонн).
Минимальный начальный запас, гарантирующий бездефицитную работу предприятия, равен:
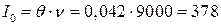 (тонн).
(тонн).
Моменты размещения заказов (повторения заказов):
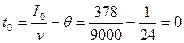 ; t1=12 дней; t2=24 дня, …
; t1=12 дней; t2=24 дня, …
Минимальные среднегодовые издержки на размещение заказов и содержание запасов составят:
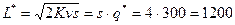 (ден. ед.).
(ден. ед.).
График динамики изменения уровня запаса и фиктивного уровня запаса при 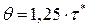 (
(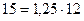 ), представлен на рис. 9.5.
), представлен на рис. 9.5.
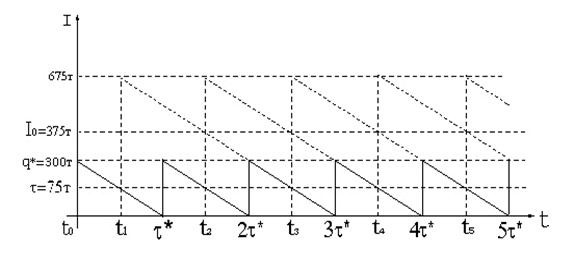
Рис. 9.5
Из графика видно, что в интервале (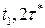 ) два заказа не выполнено, а в интервале
) два заказа не выполнено, а в интервале 
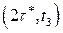 не выполнен один заказ. В интервале
не выполнен один заказ. В интервале 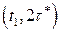 величина заказанного сырья равна
величина заказанного сырья равна 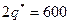 т, а в интервале
т, а в интервале 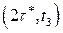 - q*=300. Средний объем потребности в сырье равен
- q*=300. Средний объем потребности в сырье равен 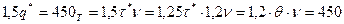 т, что больше величины потребности в сырье за время реализации заказа. Средний уровень фиктивной потребности в сырье равен:
т, что больше величины потребности в сырье за время реализации заказа. Средний уровень фиктивной потребности в сырье равен:

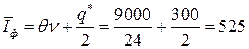 (тонн).
(тонн).
9.2.4. Учет дискретности спроса 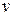 . Ранее мы предполагали, что спрос
. Ранее мы предполагали, что спрос 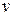 является непрерывной величиной. В действительности же требования дискретны. Тогда оптимальная партия поставки
является непрерывной величиной. В действительности же требования дискретны. Тогда оптимальная партия поставки 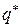 должна быть целочисленной величиной и ее можно найти из условий:
должна быть целочисленной величиной и ее можно найти из условий:

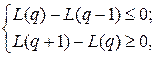
поскольку L(q*) принимает минимальное значение. Подставив значение 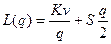 , получим систему неравенств:
, получим систему неравенств:
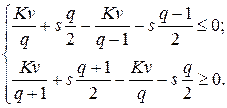
Решив систему относительно  , находим:
, находим:
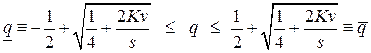 (9.3)
(9.3)
Учитывая, что 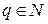 , получим
, получим 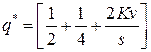 (где
(где 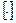 - целая часть числа) для случая, когда
- целая часть числа) для случая, когда 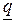 и
и 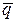 не натуральные числа. Если
не натуральные числа. Если 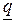 и
и 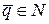 , то оптимальных решений два:
, то оптимальных решений два: 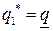 и
и 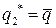 .
.
Зная оптимальную партию поставки, находим оптимальный интервал возобновления заказа 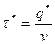 , который может быть не целочисленный. Поэтому выразим функцию издержек
, который может быть не целочисленный. Поэтому выразим функцию издержек 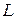 через
через 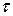 и составим систему неравенств для определения
и составим систему неравенств для определения 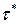 . Последовательно получаем
. Последовательно получаем

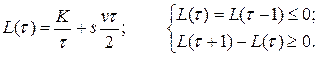
Решая систему, определяем неравенство для 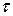 :
:

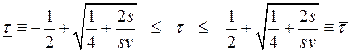 .
.
Из этого неравенства находим или одно оптимальное значение 
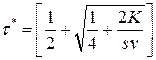 (
(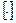 - целая часть числа) или два оптимальных решения
- целая часть числа) или два оптимальных решения 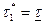 и
и 
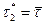 , если
, если 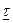 и
и 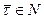 .
.
Пусть 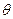 - время реализации заказа,
- время реализации заказа, 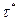 - оптимальный целочисленный период возобновления заказа,
- оптимальный целочисленный период возобновления заказа, 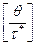 - число циклов, вмещающихся на промежутке
- число циклов, вмещающихся на промежутке 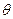 . Тогда точка размещения заказа будет вычисляться по формуле:
. Тогда точка размещения заказа будет вычисляться по формуле:
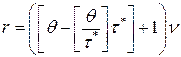 ,
,
а моменты повторения заказа, по формуле:
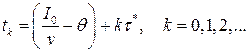
где 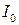 – начальный запас,
– начальный запас, 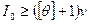
Пример 9.2. Завод поставляет заказчику станки. Средняя потребность – 2 станка в год. Стоимость организации заказа К = 30 ден. ед. Издержки содержания, включая потери от иммобилизации средств в заказах s = 10 ден. ед. в год за один станок. Определить оптимальную партию поставки.
Решение. Поскольку станки – неделимая продукция, то воспользуемся формулой (9.3) для определения оптимальной партии поставки:
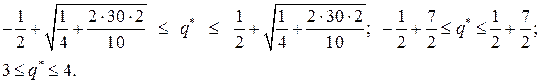
Следовательно, оптимальных решений два: 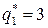 и
и 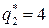 . При
. При 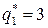 ,
, 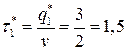 (года),
(года), 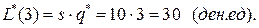 При
При 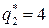 ,
, 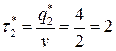 (года),
(года), 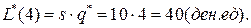
9.2.5. Модели с конечной интенсивностью поступления заказа. В предыдущих моделях предполагалось, что партия заказа  поступает мгновенно. Однако в ряде случаев выгоднее доставлять партию по частям с интенсивностью
поступает мгновенно. Однако в ряде случаев выгоднее доставлять партию по частям с интенсивностью 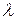 . Система может работать без дефицита, если интенсивность поставок значительно превосходит интенсивность потребления
. Система может работать без дефицита, если интенсивность поставок значительно превосходит интенсивность потребления 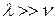 . Величина
. Величина 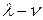 будет показывать скорость увеличения количества продукции на складе.
будет показывать скорость увеличения количества продукции на складе.
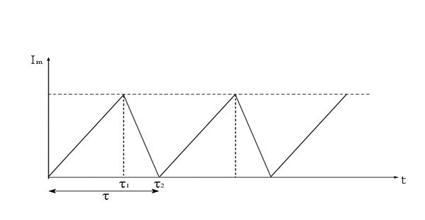
Рис 9.6
Динамика уровня запаса (рис. 9.6) характеризуется следующими предположениями:
- в начальный момент времени запас равен нулю;
-в течение времени 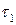 запас одновременно и поступает и расходуется (это время накопления запаса);
запас одновременно и поступает и расходуется (это время накопления запаса);
- в течение времени 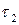 запас только расходуется (это время расходования запаса).
запас только расходуется (это время расходования запаса).
Длина цикла 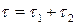 . Максимальный наличный запас будет равен:
. Максимальный наличный запас будет равен:
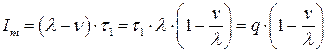 ,
, 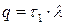 .
.
Издержки системы в единицу времени являются функцией 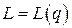 и равны сумме двух слагаемых:
и равны сумме двух слагаемых:
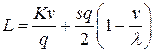 .
.
Вычислив производную 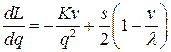 , приравняв ее к нулю
, приравняв ее к нулю
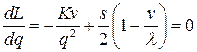 , найдем величину оптимальной партии поставки:
, найдем величину оптимальной партии поставки:
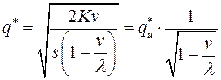 .
.
Оптимальный период возобновления заказа:
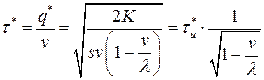
и его составляющие:
- время накопления запаса
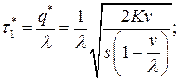
- время расходования запаса
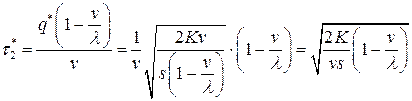 .
.
Минимальные издержки в единицу времени равны
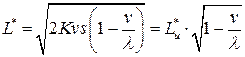 ,
,
(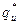 ,
, 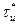 ,
, 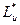 - оптимальные параметры модели Уилсона).
- оптимальные параметры модели Уилсона).
В случае, 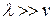 , когда интенсивность поставки значительно больше интенсивности потребления, то
, когда интенсивность поставки значительно больше интенсивности потребления, то 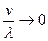 и оптимальные параметры этой модели будут равны оптимальным параметрам модели Уилсона.
и оптимальные параметры этой модели будут равны оптимальным параметрам модели Уилсона.
Предположим, что на выполнение заказа требуется время 
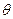 . Тогда если
. Тогда если 
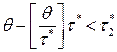 , то точка заказа вычисляется по формуле:
, то точка заказа вычисляется по формуле: 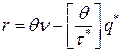 . Если же
. Если же 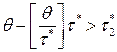 , то точка заказа равна:
, то точка заказа равна: 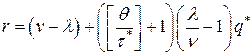 .
.
Моменты повторения заказа вычисляются по формуле
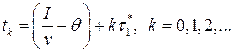
Модель оптимальной партии с конечной интенсивностью поступления может быть использована при определении оптимальной партии запуска продукции в производство. При этом К определяют издержки переналадки оборудования.
Пример 9.3. Фирма по производству соков выпускает партиями 10 различных сортов (соков) на одном и том же оборудовании. Спрос на каждый вид соков известен и составляет 5000 л. в год. Фиксированные издержки переналадки (связаны с очисткой и некоторой перенастройкой оборудования перед выработкой данного вида соков) равны 500 ден. ед. Стоимость содержания 1000 л. равная 20 ден. ед. в год. Производительность фирмы – 50000 л. в год. Время реализации заказа (от его получения до выдачи готовой продукции) – 1,5 месяца. Определить оптимальный размер партии производства одного вида соков, минимальный период возобновления производства партии одного вида сока, точку заказа и среднегодовые издержки исходя из того, что дефицит запаса на складе фирмы не допускается. Построить графическую модель изменения динамики производства соков.
Решение. В задаче определены начальные данные:
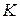 = 500 ден. ед.; n = 5000 л. в год; l = 50000 л. в год; s = 20 ден. ед. за 1000 л. в год; q=1,5 мес. =0,125 года.
= 500 ден. ед.; n = 5000 л. в год; l = 50000 л. в год; s = 20 ден. ед. за 1000 л. в год; q=1,5 мес. =0,125 года.
Применим модель с конечной интенсивностью поступления заказа и найдем оптимальные параметры работы фирмы:
- минимальная партия производства одного вида сока:
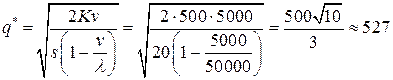 (литров);
(литров);
- время производства партии одного вида сока:
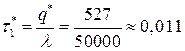 года
года 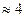 (дня);
(дня);
- время реализации партии одного вида сока:
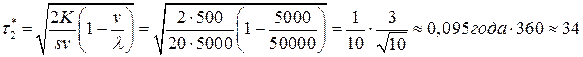 дня;
дня;
- минимальный период возобновления производства партии одного вида сока:
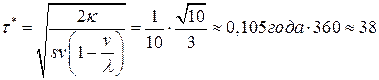 дней;
дней;
-минимальные издержки работы фирмы по производству соков за год составят:
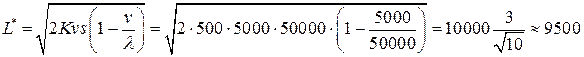 (ден. ед.).
(ден. ед.).
Поскольку 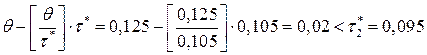 , то точку заказа вычислим по формуле:
, то точку заказа вычислим по формуле:
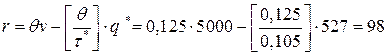 (литров).
(литров).
Если предположить, что фирма работает в стационарном режиме и начала поставлять очередную партию с 1 января, то следующая партия должна быть размещена в момент 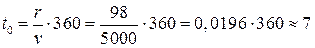 (января). Следующие заказы должны быть размещены в моменты
(января). Следующие заказы должны быть размещены в моменты 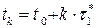 :
:

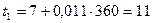 (января);
(января); 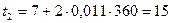 (января) и т.д.
(января) и т.д.
Для построения графика изменения динамики найдем максимальный уровень наличного запаса:
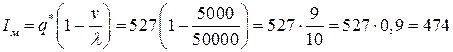 (литра).
(литра).



Рис. 9.7
9.2.6. Модель с дефицитом, когда неудовлетворенные требования ставятся на учет. В случае, когда потери из-за дефицита сравнимы с издержками хранения, дефициты допускаются. При этом требования, поступающие в моменты дефицита, берутся на учет. При прибытии очередной партии поставки сначала удовлетворяется задолженный спрос, а затем остальные требования по мере поступления. Динамика изменения уровня запаса, в предположении что  - партия поставки, характеризуется следующим образом.
- партия поставки, характеризуется следующим образом.
В начальный момент времени уровень запаса равен максимальной величине наличного запаса 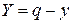 , где
, где 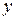 - величина задолженного спроса. Наличный запас расходуется за время
- величина задолженного спроса. Наличный запас расходуется за время 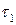 , которое называется временем существования наличного запаса. Затем поступающие требования берутся на учет в течение времени
, которое называется временем существования наличного запаса. Затем поступающие требования берутся на учет в течение времени 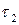 , называемым временем дефицита. При поступлении очередной партии в первую очередь удовлетворяется задолженный спрос, а затем пополняется запас (см. рис. 9.8).
, называемым временем дефицита. При поступлении очередной партии в первую очередь удовлетворяется задолженный спрос, а затем пополняется запас (см. рис. 9.8).
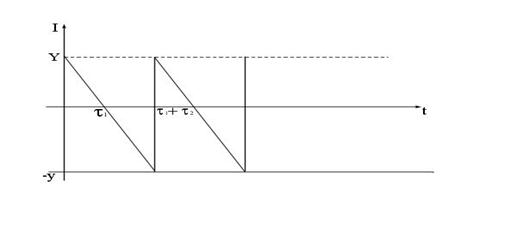
Рис. 9.8
Убытки, связанные с дефицитом единицы запаса в единицу времени, обозначим 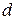 . Тогда издержки цикла состоят:
. Тогда издержки цикла состоят:
· из издержек 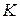 размещения заказа, не зависящих от величины партии
размещения заказа, не зависящих от величины партии  ;
;
· из издержек на хранение продукции, пропорциональных средней величине запаса 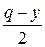 и времени его существования
и времени его существования 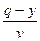 ;
;
· из издержек от дефицита, пропорциональных средней величине дефицита 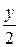 и времени его существования
и времени его существования 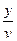 , т.е.
, т.е. 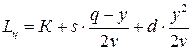 .
.
Разделим издержки цикла на его величину 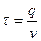 и получим издержки работы системы в единицу времени:
и получим издержки работы системы в единицу времени:
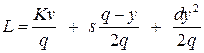 . (9.4)
. (9.4)
Издержки работы системы в единицу времени являются функцией двух переменных  и
и 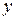 , т.е.
, т.е. 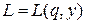 . Применив необходимые условия экстремума функции 2-ух переменных, т. е. вычислив частные производные
. Применив необходимые условия экстремума функции 2-ух переменных, т. е. вычислив частные производные
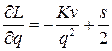
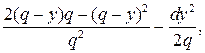
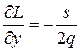
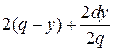 .
.
и приравняв их нулю, получим систему:
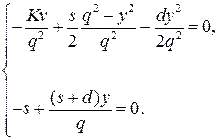
Решив систему, находим оптимальные значения  и
и 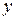 :
:
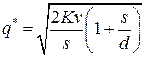 ;
; 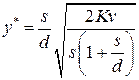
Вычислив частные производные второго порядка 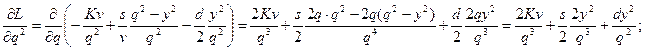
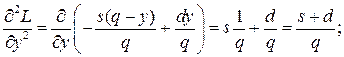
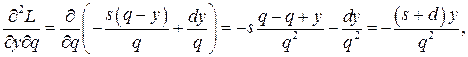
и их значения при 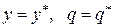
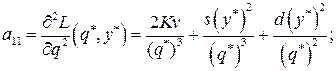
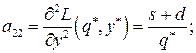
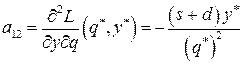
составим выражение
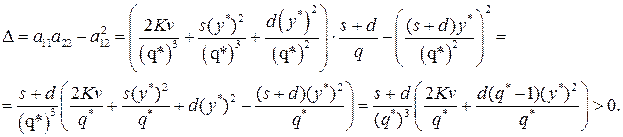
Так как 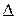 > 0 и
> 0 и 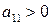 , то при
, то при 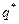 и
и 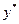 издержки достигают минимального значения.
издержки достигают минимального значения.
Подставив найденные значения 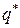 и
и 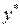 в формулу (9.4),найдем минимальные издержки работы системы:
в формулу (9.4),найдем минимальные издержки работы системы:
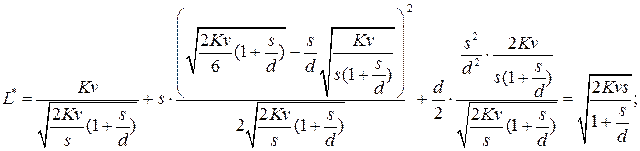
Зная оптимальные значения 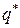 и
и 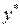 , найдем:
, найдем:
-максимальный уровень наличного запаса
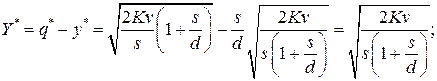
- время существования наличного запаса
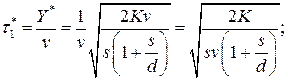
- время существования дефицита
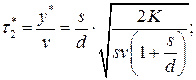
- длину цикла

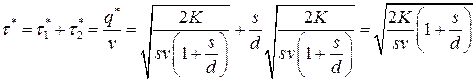 .
.
Отметим, что в рассматриваемой модели
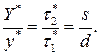
Кроме того, при высоких штрафах за дефицит, когда 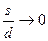 , рассматриваемая модель превращается в модель Уилсона. Когда неудовлетворенные требования ставятся на учет, точка заказа может быть рассчитана по формуле:
, рассматриваемая модель превращается в модель Уилсона. Когда неудовлетворенные требования ставятся на учет, точка заказа может быть рассчитана по формуле:
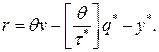
Поскольку 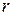 может быть отрицательной величиной, то заказ должен размещаться в момент, когда величина требований, поставленных на учет, равна
может быть отрицательной величиной, то заказ должен размещаться в момент, когда величина требований, поставленных на учет, равна 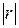 .
.
Пример 9.4. Спрос на продукцию составляет 1900 тонн в год. Стоимость хранения, включая потери от иммобилизации средств в запасах и связанные со снижением цен, в случае нереализации продукции, равна 19 ден. ед. за 1 тонну в год. Издержки размещения заказа составляют 200 ден. ед. Неудовлетворенные требования берутся на учет. Удельные издержки дефицита составляют 81 ден. ед. за нехватку 1 тонны в течение года. Среднее время реализации заказа – 1 месяц. Определить оптимальную партию поставки, максимальную величину размещения заказа и минимальные издержки функционирования системы. Построить графическую модель изменения динамики спроса на продукцию.
Решение. В задаче определены начальные данные: 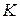 = 200 ден. ед.;
= 200 ден. ед.; 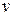 = 1900 тонн в год; s = 19 ден. ед. за 1 тонну в год;
= 1900 тонн в год; s = 19 ден. ед. за 1 тонну в год; 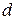 = 81 ден. ед. за нехватку 1 тонны в год;
= 81 ден. ед. за нехватку 1 тонны в год; 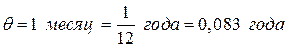 .
.
Применим модель с дефицитом и найдем оптимальные параметры работы системы:
- минимальную партию поставки продукции:
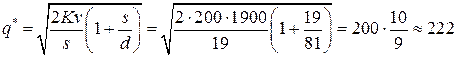 (тонны);
(тонны);
-максимальную величину задолженного спроса
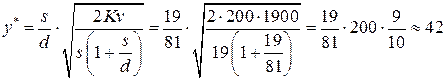 (тонны);
(тонны);
- максимальную величину наличного запаса
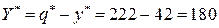 (тонн);
(тонн);
-оптимальную величину цикла (минимальную величину возобновления заказа, интервал возобновления заказа)
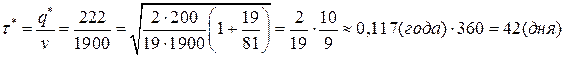 ;
;
- время существования наличного запаса
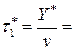
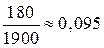 (года) = 0,095
(года) = 0,095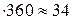 (дня);
(дня);
- время существования дефицита
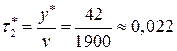 (года) =
(года) = 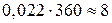 (дней);
(дней);
- точку заказа
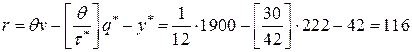 (тонн);
(тонн);
-минимальные издержки работы системы

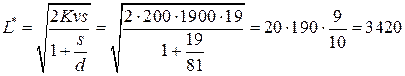 (ден. ед. в год).
(ден. ед. в год).
Динамика изменения уровня запаса изображена на рис. 9. 9.

Рис. 9.9
9.2.7. Обобщенная модель оптимальной партии поставки с постоянной интенсивностью и с учетом неудовлетворенных требований. Рассмотрим модель с постоянной интенсивностью спроса 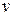 и постоянной интенсивностью поступления
и постоянной интенсивностью поступления 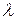 единиц в единицу времени. Предположим, что потери из-за дефицита сравнимы с издержками хранения. Тогда дефицит допускается, причем неудовлетворенные требования накапливаются и по мере новых поступлений удовлетворяются. Динамика изменения уровня запаса в этом случае показана на рис. 9.10 и характеризуется следующими положениями:
единиц в единицу времени. Предположим, что потери из-за дефицита сравнимы с издержками хранения. Тогда дефицит допускается, причем неудовлетворенные требования накапливаются и по мере новых поступлений удовлетворяются. Динамика изменения уровня запаса в этом случае показана на рис. 9.10 и характеризуется следующими положениями:
- в начальный момент времени уровень запаса равен нулю, 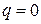 ;
;
- в течение времени 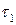 запас одновременно поступает и расходуется - это время накопления запаса;
запас одновременно поступает и расходуется - это время накопления запаса;
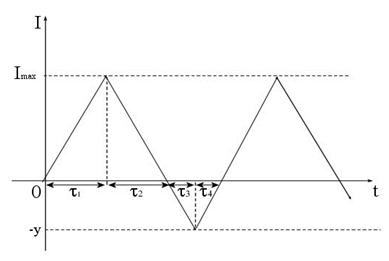
Рис. 9.10
- в течение времени 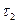 запас только расходуется до нуля - это время расходования запаса;
запас только расходуется до нуля - это время расходования запаса;
- в течение времени 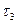 поступающие требования ставятся на учет - это время накапливания дефицита;
поступающие требования ставятся на учет - это время накапливания дефицита;
- в течение времени 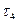 поступает новая партия с интенсивностью
поступает новая партия с интенсивностью 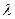 и ликвидируется дефицит - это время ликвидации дефицита, затем идет накопления запаса и т. д.
и ликвидируется дефицит - это время ликвидации дефицита, затем идет накопления запаса и т. д.
Пусть  величина партии поставки. Тогда
величина партии поставки. Тогда 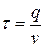 и
и 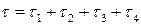 .
.
Пусть s – затраты содержания единицы продукции в единицу времени, а 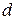 - затраты дефицита единицы запаса в единицу времени. Из экономических соображений следует, что отношение максимального уровня наличного запаса к максимальной величине дефицита
- затраты дефицита единицы запаса в единицу времени. Из экономических соображений следует, что отношение максимального уровня наличного запаса к максимальной величине дефицита 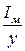 равно отношению
равно отношению 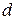 к
к 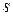 , т.е.
, т.е. 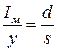 . Этому же отношению равно и отношение времени расходования запаса и времени накапливания дефицита. Максимальный уровень наличного запаса равен
. Этому же отношению равно и отношение времени расходования запаса и времени накапливания дефицита. Максимальный уровень наличного запаса равен 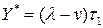 . Эта величина запаса полностью расходуется за время
. Эта величина запаса полностью расходуется за время 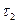 . Поэтому
. Поэтому 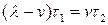 . Накопление максимальной величины дефицита идет со скоростью равной потреблению в течение времени
. Накопление максимальной величины дефицита идет со скоростью равной потреблению в течение времени 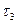 , т.е.
, т.е. 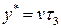 . Дефицит ликвидируется при поступлении новой партии со скоростью
. Дефицит ликвидируется при поступлении новой партии со скоростью 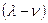 в течение времени
в течение времени 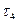 , т.е.
, т.е. 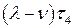 . Поэтому
. Поэтому 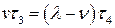 . Таким образом, получим систему из четырех уравнений, относительно
. Таким образом, получим систему из четырех уравнений, относительно 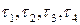 .
.
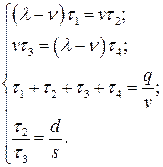
Решив систему относительно 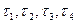 , получим:
, получим: 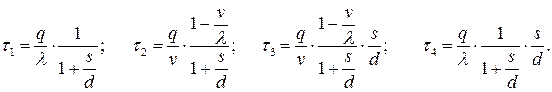
Издержки работы системы состоят из:
- издержек размещения заказа K, не зависящих от величины партии;
-издержек содержания запаса пропорциональных средней величине запаса 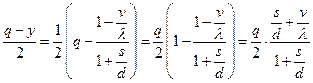
и времени его существования 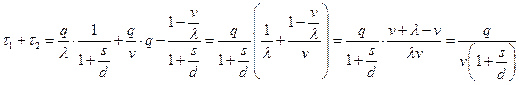 ;
;
- издержек от дефицита, пропорциональных средней величине дефицита 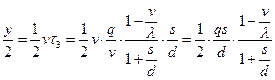
и времени его существования 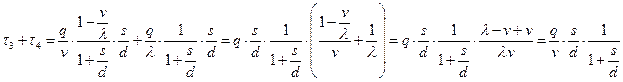
Тогда общие издержки в течение цикла равны сумме издержек от реализации заказа, содержания запасов и от дефицита:
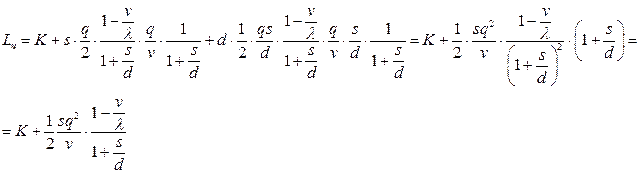
Разделив издержки цикла на величину цикла 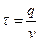 , получим издержки функционирования системы в единицу времени:
, получим издержки функционирования системы в единицу времени:
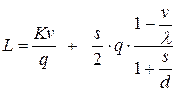 .
.
Это функция от величины  партии поставки
партии поставки 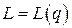 . Вычислим производную по
. Вычислим производную по  , приравняв ее к нулю, найдем
, приравняв ее к нулю, найдем 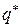 :
:
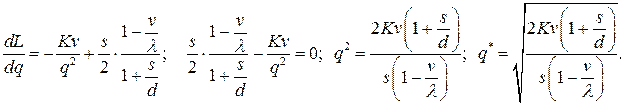
Это минимум функции 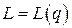 , так как
, так как 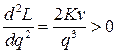 . Воспользовавшись найденным значением q*, находим:
. Воспользовавшись найденным значением q*, находим:
- максимальный уровень наличного запаса
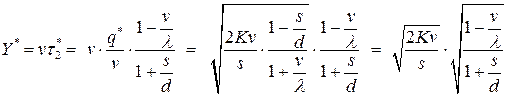 ;
;
- максимальный уровень дефицита
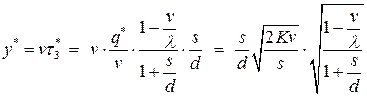 ;
;
- минимальный период возобновления заказа
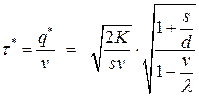 ;
;
- минимальные издержки функционирования системы в единицу времени
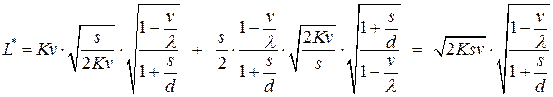 .
.
Пример 9.5. Фирма 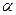 выпускает партиями изделия пяти типов по 1500 штук в сутки. Средний объем потребления каждого типа изделия – 300 штук в сутки. Стоимость переналадки оборудования при переходе от одного типа изделия к другому составляет 1200 ден. ед. Стоимость содержания одного изделия 0,03 ден. ед. в сутки. Неудовлетворенные требования берутся на учет. Удельные издержки дефицита составляют 0,15 ден. ед. за изделие в сутки. Определить оптимальные параметры работы фирмы
выпускает партиями изделия пяти типов по 1500 штук в сутки. Средний объем потребления каждого типа изделия – 300 штук в сутки. Стоимость переналадки оборудования при переходе от одного типа изделия к другому составляет 1200 ден. ед. Стоимость содержания одного изделия 0,03 ден. ед. в сутки. Неудовлетворенные требования берутся на учет. Удельные издержки дефицита составляют 0,15 ден. ед. за изделие в сутки. Определить оптимальные параметры работы фирмы 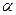 .
.
Решение. В условии задачи заданы: интенсивность поступления 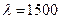 изделий в сутки; спрос
изделий в сутки; спрос 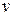 = 300 изделий в сутки; издержки переналадки оборудования
= 300 изделий в сутки; издержки переналадки оборудования 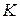 = 1200 ден. ед., издержки содержания s = 0,03 ден. ед. в сутки, издержки дефицита
= 1200 ден. ед., издержки содержания s = 0,03 ден. ед. в сутки, издержки дефицита 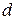 = 0,15 ден. ед. в сутки.
= 0,15 ден. ед. в сутки.
Воспользуемся моделью с постоянной интенсивностью поступления и спроса, когда неудовлетворенные поступления берутся на учет. Тогда минимальная партия поставки:
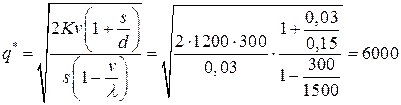 (изделий);
(изделий);
- минимальный уровень наличного запаса:
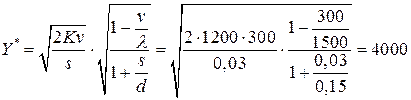 (изделий);
(изделий);
- максимальный уровень дефицита:
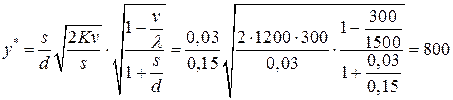 (изд.);
(изд.);
- минимальный период возобновления заказа:
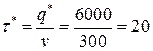 (суток);
(суток);
- время накопления и расходования:
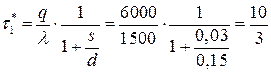 (суток);
(суток);
- время расходования:
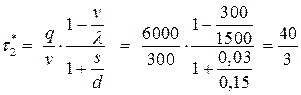 (суток);
(суток);
- время накопления дефицита:
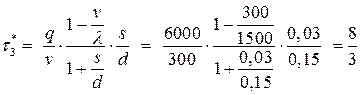 (суток);
(суток);
- время ликвидации дефицита:
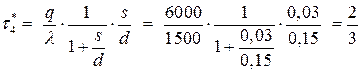 (суток).
(суток).
Условие 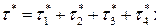
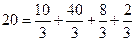 , выполняется.
, выполняется.
Минимальные издержки работы фирмы за сутки равны:
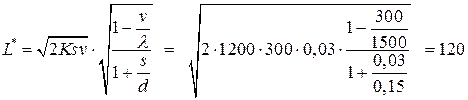 (ден. ед.)
(ден. ед.)
Время, которое необходимо на производство одной партии: 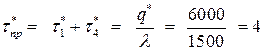 (суток).
(суток).
Так как 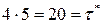 , то мощность фирмы позволяет наладить выпуск пяти типов изделий партиями по
, то мощность фирмы позволяет наладить выпуск пяти типов изделий партиями по 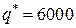 изделий.
изделий.
9.2.8. Модель в условиях скидки на размер заказа. Для увеличения объема продажи фирмы предлагают количественные скидки, т.е. снижение цены при оптовых закупках. Скидка может быть оптовой и дифференциальной.
Рассмотрим случай оптовой скидки, когда с увеличением размера заказываемой партии  уменьшается стоимость каждой единицы товара. Предположим, что величина заказываемой партии может быть либо
уменьшается стоимость каждой единицы товара. Предположим, что величина заказываемой партии может быть либо 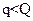 , либо
, либо 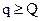 , где
, где 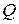 некоторый объем продукции. При
некоторый объем продукции. При 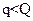 , стоимость единицы продукции равна
, стоимость единицы продукции равна 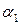 , а при
, а при 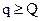 стоимость единицы продукции равна
стоимость единицы продукции равна 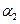 , причем
, причем 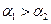 .
.
При 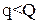 издержки работы системы в течении цикла состоят из:
издержки работы системы в течении цикла состоят из:
- издержек размещения заказа 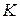 ;
;
- издержек содержания 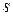 единицы заказа в единицу времени, как процент от стоимости единицы продукции
единицы заказа в единицу времени, как процент от стоимости единицы продукции 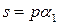 , где
, где 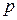 – стоимость содержания выраженная в процентах от стоимости единицы продукции
– стоимость содержания выраженная в процентах от стоимости единицы продукции 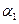 ;
;
- стоимости единицы продукции 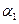 партии
партии 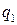 :
:
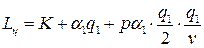 .
.
Разделив издержки на длину цикла, получим издержки в единицу времени:
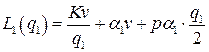 .
.
Аналогично, при 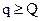 издержки в единицу времени равны:
издержки в единицу времени равны:
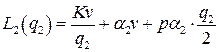 .
.
Вычислив производные
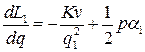 ,
, 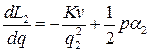 ,
,
приравняв их к нулю
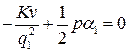 и
и 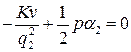
найдем значения 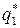 и
и 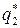
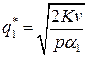 и
и 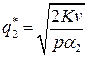
и минимальные издержки
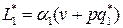 и
и 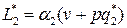 .
.
Имеются два значения  оптимальной партии поставки. Для выбора соответствующего значения
оптимальной партии поставки. Для выбора соответствующего значения  рассмотрим различные случаи значений
рассмотрим различные случаи значений 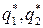 и Q, алгоритм их сравнения и выбора оптимальной партии.
и Q, алгоритм их сравнения и выбора оптимальной партии.
1. Вычисляем 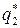 . Если
. Если 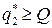 , то учитывая, что
, то учитывая, что 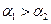 , оптимальной партией будет
, оптимальной партией будет 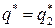 .
.
2. Если 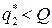 , то вычисляем
, то вычисляем 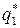 и разность
и разность 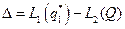 , где
, где 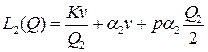 . Если
. Если 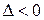 , то
, то 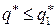 . Если
. Если 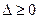 , то
, то 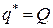 .
.
Эти выводы можно пояснить на рис.9.11 (а, б, в).
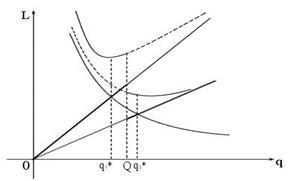
а)
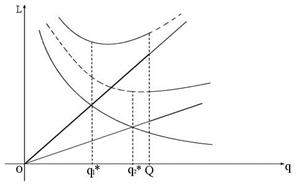
б)
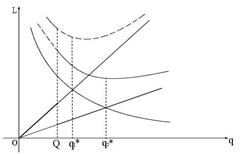
в)
Рис. 9.11
Пусть 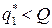 и
и 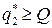 (рис.9.11, а), то сравниваем
(рис.9.11, а), то сравниваем 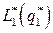 и
и 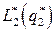 . Если
. Если 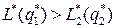 и учитывая, что
и учитывая, что 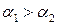 , определяем оптимальную партию
, определяем оптимальную партию 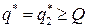 . Пусть
. Пусть 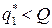 и
и 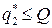 . Тогда для определения оптимальной партии сравниваем
. Тогда для определения оптимальной партии сравниваем 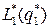 с
с 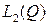 : если
: если 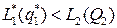 , то
, то 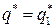 , если
, если 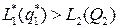 , то
, то 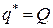 , если
, если 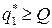 и
и 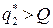 , то
, то 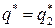 .
.
Пример 9.6. Сборочное предприятие заказывает подшипники заводу. Спрос на них 5000 ед. в год. Подшипниковый завод выпускает различные подшипники партиями. Стоимость переналадки составляет 500 ден. ед. Если заказ не превышает 2000
 2014-02-09
2014-02-09 4681
4681

 2𝜏
2𝜏