Одноэлектронное уравнение Шредингера для кристалла. Одноэлектронная волновая функция Блоха

Раздел 2. Электронные состояния и движение электронов в идеальном кристалле.

2.1 Одноэлектронное уравнение Шредингера для кристалла. Одноэлектронная волновая функция Блоха.

2.2 Методы расчета электронных энергетических состояний в твердых телах. Приближения свободных и сильносвязанных электронов.

2.3 Зонная структура твердых тел. Зоны Бриллюэна для кубических и генксагональных кристаллов.

2.4 Эффективная масса электрона в кристалле, её связь со структурой энергетических зон. Понятие дырки. Динамика электрона в периодическом поле изитропных и анизотропных кристаллов.

2.5 Зонная структура типичных металлов, полупроводников, полуметаллов, бесщелевых полупроводников и диэлектриков.

2.6 Размерное квантование энергии электронов и дырок в полупроводниках. Квантоворазмерные структуры с низкоразмерным электронным газом.

Электронный спектр кристалла –зависимость энергии электрона в периодическом потенциальном поле кристалла от волнового вектора k электрона (или закон дисперсии)

Закон дисперсии для свободного электрона

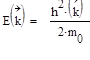, mо – масса свободного электрона

k - волновой вектор, который указывает направление движения электрона в пространстве.

Движение свободного электрона описывается как распространение плоской электронной волны (волны де Бройля).

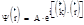
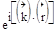- фазовый показатель.

А- амплитуда.

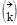- расстояние.

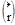- волновой вектор.

В кристалле: энергия электрона изменяется под действием сил поля решетки – закон дисперсии из непрерывного превращается в набор разрешенных и запрещенных зон энергии, а также изменяется масса электрона: она может быть больше или меньше m_о, а также быть положительной или отрицательной. Массу электрона в кристалле называют эффективной, она не имеет отношения к силам тяготения, но описывает динамику электрона в кристалле.

Обозначение m* -величина изотропная или тензорная в зависимости от типа кристаллов.

Движение электрона описывается бегущей плоской электронной волной с модулированной амплитудой с периодом решетки:

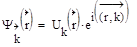- волна Блоха.

Зонный характер электронного спектра можно понять из рассмотрения образования кристалла в квантовой(зонной) теории ТТ:

Образует кристалл ∞-ных размеров без дефектов(идеальный) из изолированных атомов.

Изолированные атомы имеют известный электронный спектр - набор дискретных уровней энергии Еn (n – номер уровня)

Расположим атомы в виде кристаллической решетки необходимой симметрии, но с расстояниями между атомами d > a (a - const решетки)

Тогда каждый уровень En будет повторяться N- раз по числу атомов в единице объёма или иначе каждый уровень будет N- кратно вырожден.

Сблизим атомы (однородным сжатием решетки) до расстояния d=a.В этом случае – вырождение уровней Еn – снимается путем расщепления каждого уровня в зону, состоящей из N –уровней в результате обменного взаимодействия между атомами (см рис 2).

Теперь электрон переходит от атома к атому в результате тунеллирования и,т.о. – он принадлежит уже всей совокупности атомов – т.е. свободно перемещается по кристаллу.

Рис. 2. Образование зонного спектра.

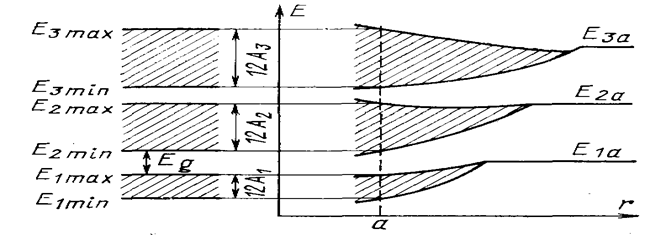
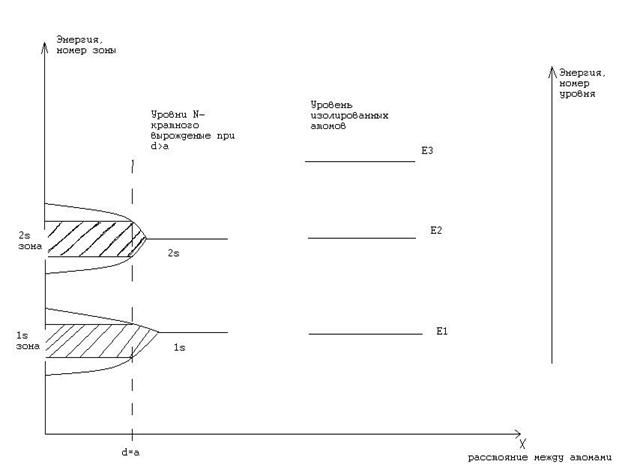
Выберем уровни 1s и 2s

Из уровня 1s образуется 1s зона, а из уровня 2s 2s-зона разрешенных значений энергии для е в кристалле, между 1s и 2s зонами имеет место запрещенные значения энергии для е в кристалле- запрещенная зона.

Т.о. получаем чередование разрешенных и запрещенных зон энергии – зонная структура Т.Т.

Зонные модели металлов, диэлектриков, полупроводников.

Металлы: к металлам относят вещества, у которых верхняя зона, заполняемая электронами, не полностью заполнена.

Это происходит, если разрешенная зона образуется из атомов энергетического уровня, не заполненного электронами.

У типичных металлов верхняя зона возникает из s – состояния, в котором находится 1 электрон.

В кристалле s- зона содержит 2N – состояний, поэтому s – зона будет заполнена на ½.