Рассмотрим процесс равновесного (без трения) адиабатного истечения газа через сопло из резервуара, в котором газ имеет параметры Т1 , p 1, v 1.Скорость газа на входе в сопло обозначим через c 1. Будем считать, что давление газа на выходе из сопла р 2 равно давлению среды, в которую вытекает газ.
Расчет сопла сводится к определению скорости и расхода газа на выходе из него, нахождению площади поперечного сечения и правильному выбору его формы.
Скорость истечения в соответствии с уравнением (7.5)
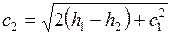 .
.
Выберем достаточно большую площадь входного сечения сопла, тогда c1 =0 и
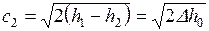
где  — располагаемый адиабатный теплоперепад.
— располагаемый адиабатный теплоперепад.
Для идеального газа изменение внутренней энергии в адиабатном процессе 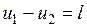 вычисляется по формуле
вычисляется по формуле 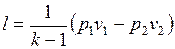 , поэтому
, поэтому
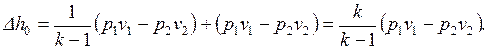
Тогда
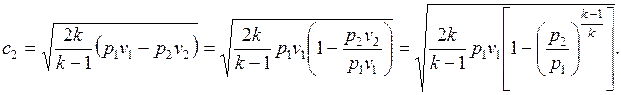 (7.6)
(7.6)
Массовый расход газа т через сопло (кг/с) определяется из соотношения
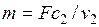 , (7.7)
, (7.7)
где F — площадь выходного сечения сопла.
Воспользовавшись выражениями (7.6) и (7.7), получим
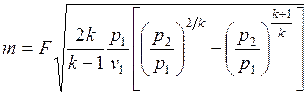 . (7.8)
. (7.8)
Из выражения (7.8) следует, что массовый расход идеального газа при истечении зависит от площади выходного сечения сопла, свойств и начальных параметров газа и степени его расширения (т. е. давления газа на выходе).
По уравнению (7.8) построена кривая 1K0.
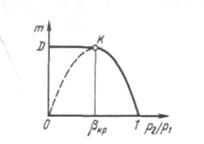
Рисунок 7.3 - Зависимость массового расхода газа через сопло от отношения
При p 2= p 1 расход, естественно, равен нулю. С уменьшением давления среды p 2расход газа увеличивается и достигает максимального значения при 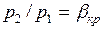 . При дальнейшем уменьшении отношения
. При дальнейшем уменьшении отношения 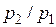 значение т, рассчитанное по формуле (7.8), убывает и при
значение т, рассчитанное по формуле (7.8), убывает и при 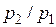 =0 становится равным нулю.
=0 становится равным нулю.
Сравнение описанной зависимости с экспериментальными данными показало, что для результаты полностью совпадают, а для они расходятся—действительный массовый расход на этом участке остается постоянным (прямая KD).
Для того чтобы объяснить это расхождение теории с экспериментом, А. Сен-Венан в 1839 г. выдвинул гипотезу о том, что в суживающемся сопле невозможно получить давление газа ниже некоторого критического значения р кр, соответствующего максимальному расходу газа через сопло. Как бы мы ни понижали давление р 2 среды, куда происходит истечение, давление на выходе из сопла остается постоянным и равным р кр.
Для отыскания максимума функции 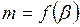 (при p 1=const), соответствующего значению
(при p 1=const), соответствующего значению 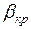 , возьмем первую производную от выражения в квадратных скобках и приравняем ее нулю:
, возьмем первую производную от выражения в квадратных скобках и приравняем ее нулю:
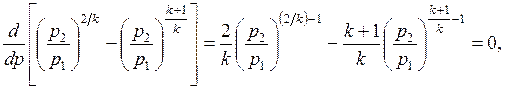
откуда
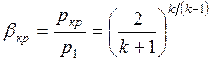 . (7.9)
. (7.9)
Таким образом, отношение критического давления на выходе к давлению перед соплом имеет постоянное значение и зависит только от показателя адиабаты, т. е. от природы рабочего тела.
| Газ | 1-атомный | 2-атомный | 3-атомный и перегретый пар |
| k | 1,66 | 1,4 | 1,3 |
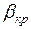 | 0,49 | 0,528 | 0,546 |
Таким образом, изменение невелико, поэтому для оценочных расчетов можно принять 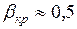 .
.
Критическая скорость устанавливается в устье сопла при истечении в окружающую среду с давлением, равным или ниже критического. Ее можно определить по уравнению:
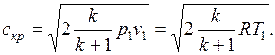 (7.10)
(7.10)
Величина критической скорости определяется физическими свойствами и начальными параметрами газа.
Из уравнения адиабаты следует, что 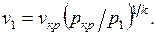 Заменяя здесь отношение
Заменяя здесь отношение 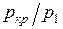 в соответствии с уравнением (7.9), получаем
в соответствии с уравнением (7.9), получаем
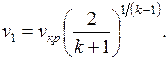
Подставляя значение v 1 и значение p 1в формулу 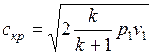 , получаем
, получаем 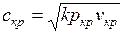 . Из курса физики известно, что
. Из курса физики известно, что 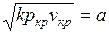 есть скорость распространения звука в среде с параметрами
есть скорость распространения звука в среде с параметрами 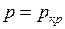 и
и 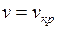 .
.
Таким образом, критическая скорость газа при истечении равна местной скорости звука в выходном сечении сопла. Именно это обстоятельство объясняет, почему в суживающемся сопле газ не может расшириться до давления, меньшего критического, а скорость не может превысить критическую.
Действительно, как известно из физики, импульс давления (упругие колебания) распространяется в сжимаемой среде со скоростью звука, поэтому когда скорость истечения меньше скорости звука, уменьшение давления за соплом передается по потоку газа внутрь канала с относительной скоростью c+a и приводит к перераспределению давления (при том же значении давления газа p 1перед соплом). В результате в выходном сечении сопла устанавливается давление, равное давлению среды.
Если же скорость истечения достигнет скорости звука (критической скорости), то скорость движения газа в выходном сечении и скорость распространения давления будут одинаковы. Волна разрежения, которая возникает при дальнейшем снижении давления среды за соплом, не сможет распространиться против течения в сопле, так как относительная скорость ее распространения (а — с) будет равна нулю. Поэтому никакого перераспределения давлений не произойдет и, несмотря на то, что давление среды за соплом снизилось, скорость истечения останется прежней, равной скорости звука на выходе из сопла.
Максимальный секундный расход газа при критическом значении 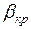 можно определить из уравнения (7.8), если в него подставить
можно определить из уравнения (7.8), если в него подставить 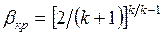 . Тогда
. Тогда
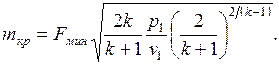 (7.11)
(7.11)
Максимальный секундный расход определяется состоянием газа на входе в сопло, величиной выходного сечения сопла 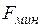 и показателем адиабаты газа, т. е. его природой.
и показателем адиабаты газа, т. е. его природой.
Все приведенные соотношения приближенно справедливы и для истечения из непрофилированных специально сопл, например из отверстий в сосуде, находящемся под давлением. Скорость истечения из таких отверстий не может превысить критическую, определяемую формулой (7.11), а расход не может быть больше определяемого при любом давлении в сосуде. (Из-за больших потерь на завихрения в этом случае расход вытекающего газа будет меньше рассчитанного по приведенным формулам).
Чтобы получить на выходе из сопла сверхзвуковую скорость, нужно придать ему специальную форму, что видно из следующего параграфа.
 2014-02-09
2014-02-09 16291
16291
