Влияние сжимаемости на форму трубок тока.
Рассмотрим, как влияет сжимаемость на форму трубок тока при установившемся движении газа. Предположим, что трубка тока тонкая, и характеристики движения в разных точках каждого сечения одинаковы. Пусть 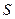 – площадь произвольного поперечного сечения трубки тока, причем сечение перпендикулярно к скорости движения частиц газа.
– площадь произвольного поперечного сечения трубки тока, причем сечение перпендикулярно к скорости движения частиц газа.

Если жидкость однородная и несжимаемая, то из уравнения неразрывности следует, что массовый и объемный расходы через трубку тока постоянны, т.е. 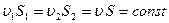 ;
; 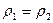 и
и
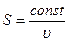 ,
,
т.е. чем больше скорость, тем меньше сечение.

В этом случае вдоль трубки должен сохраняться только массовый расход жидкости  , откуда
, откуда
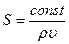 . (7.39)
. (7.39)
Для сжимаемой жидкости плотность зависит от скорости. Для обратимых адиабатических течений совершенного газа
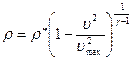 .
.
 Подставляя это выражение в (7.39), можно получить зависимость
Подставляя это выражение в (7.39), можно получить зависимость 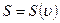 и найти форму трубок тока. График
и найти форму трубок тока. График 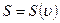 приведен на рис. 7.15. Кривая
приведен на рис. 7.15. Кривая 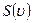 имеет две асимптоты:
имеет две асимптоты: 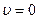 и
и 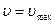 .
.
Определим форму трубок тока для любых (не адиабатических) движений идеальной сжимаемой жидкости. Вычислим 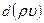 . Спроектируем уравнение движения Эйлера на линию тока и при установившемся движении
. Спроектируем уравнение движения Эйлера на линию тока и при установившемся движении
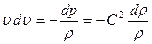 ,
,
где 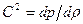 вдоль линии тока. Для адиабатических движений, как было указано ранее,
вдоль линии тока. Для адиабатических движений, как было указано ранее, 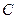 совпадает со скоростью звука, определяемой как
совпадает со скоростью звука, определяемой как 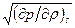 (в общем случае величина
(в общем случае величина 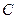 отлична от скорости звука, но в последующем для неадиабатических движений играет роль скорости звука). Таким образом, вдоль линии тока имеем
отлична от скорости звука, но в последующем для неадиабатических движений играет роль скорости звука). Таким образом, вдоль линии тока имеем
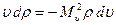 . (7.40)
. (7.40)
Отсюда
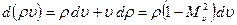 . (7.41)
. (7.41)
Видно, что с ростом скорости, когда 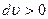 , величина
, величина 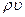 растет при дозвуковых скоростях
растет при дозвуковых скоростях 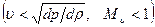 и убывает при сверхзвуковых скоростях
и убывает при сверхзвуковых скоростях 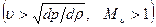 . В точке, в которой
. В точке, в которой 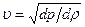 , т.е.
, т.е. 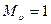 , величина
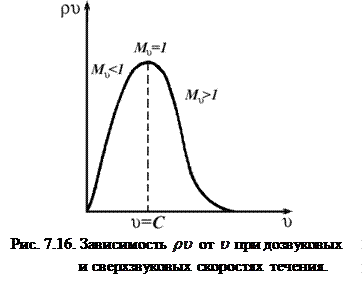
, величина 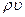 имеет максимум (рис. 7.16).
имеет максимум (рис. 7.16).
Таким образом, в дозвуковом потоке 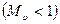 поперечное сечение трубки тока с ростом скорости
поперечное сечение трубки тока с ростом скорости 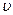 уменьшается. Максимальная скорость, которая может быть достигнута при дозвуковом потоке в сужающейся трубке тока, равна скорости звука.
уменьшается. Максимальная скорость, которая может быть достигнута при дозвуковом потоке в сужающейся трубке тока, равна скорости звука.
В сверхзвуковом потоке 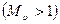 , если скорость потока вдоль трубки растет, то
, если скорость потока вдоль трубки растет, то 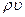 убывает, и трубка тока расширяется. Если скорость сверхзвукового потока вдоль трубки убывает, то
убывает, и трубка тока расширяется. Если скорость сверхзвукового потока вдоль трубки убывает, то 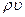 растет и поперечное сечение уменьшается, следовательно, поток в сужающемся канале замедляется.
растет и поперечное сечение уменьшается, следовательно, поток в сужающемся канале замедляется.
 |

Насадок, состоящий только лишь из сужающегося участка (рис. 7.17), называется простым соплом. Наибольшая скорость, которую можно получить, выпуская адиабатически газ через простое сопло, равна скорости звука, которая достигается в наиболее узком сечении (на срезе сопла).
 |
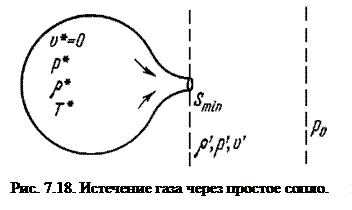
Пусть имеется большой сосуд (рис. 7.18), заполненный газом, который может вытекать из него через простое сопло в пространство с давлением 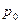 . Величина
. Величина 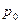 называется противодавлением. Значения характеристик течения на срезе сопла обозначим через
называется противодавлением. Значения характеристик течения на срезе сопла обозначим через 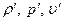 , а в сосуде далеко от насадка – через
, а в сосуде далеко от насадка – через 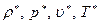 . Примем, что
. Примем, что 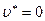 . Понятно, что если
. Понятно, что если 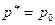 , то течения в сопле не будет.
, то течения в сопле не будет.
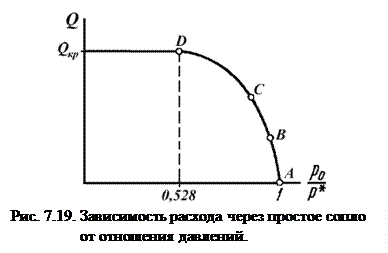
Рассмотрим, как зависит массовый расход газа 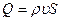 через сопло от отношения давлений
через сопло от отношения давлений  при постоянных значениях температуры
при постоянных значениях температуры 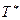 и давления
и давления 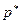 в сосуде, когда отсутствует теплообмен между газом и окружающей средой.
в сосуде, когда отсутствует теплообмен между газом и окружающей средой.
 |
 Если
Если  , то
, то 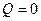 (этому случаю соответствует точка
(этому случаю соответствует точка  на рис. 7.19). При
на рис. 7.19). При  скорость течения в сопле будет дозвуковой, и наибольшее значение скорости будет достигаться на срезе сопла (например, в точке
скорость течения в сопле будет дозвуковой, и наибольшее значение скорости будет достигаться на срезе сопла (например, в точке 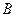 ). При дальнейшем уменьшении
). При дальнейшем уменьшении  скорость на срезе сопла, оставаясь дозвуковой, будет увеличиваться.
скорость на срезе сопла, оставаясь дозвуковой, будет увеличиваться.
При некотором значении 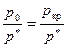 скорость на срезе сопла станет равной местной скорости звука
скорость на срезе сопла станет равной местной скорости звука  . При этом критические значения плотности и давления, согласно (7.30) и (7.34), равны:
. При этом критические значения плотности и давления, согласно (7.30) и (7.34), равны:
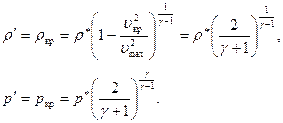 (7.42)
(7.42)
На основе экспериментальных данных известно, что до тех пор, пока 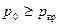 , давление на срезе сопла практически совпадает с противодавлением
, давление на срезе сопла практически совпадает с противодавлением 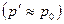 . Поэтому при достижении в минимальном сечении скорости звука можно считать, что
. Поэтому при достижении в минимальном сечении скорости звука можно считать, что
 . (7.43)
. (7.43)
При 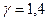 на основе (7.43) получим, что
на основе (7.43) получим, что 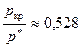 (точка
(точка 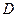 на рис. 7.19).
на рис. 7.19).
Критический расход, согласно (7.30) и (7.42), будет равен
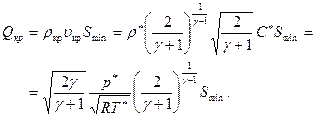 (7.44)
(7.44)
При дальнейшем понижении противодавления 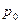 течение внутри сопла перестает меняться, и расход также остается неизменным и равным критическому. Неизменность расхода объясняется тем, что слабые возмущения (а значит, и небольшие изменения противодавления) распространяются по частицам среды со скоростью звука. Поэтому при достижении критического режима (когда сами частицы на срезе сопла имеют скорость, равную скорости звука) частицы, находящиеся внутри сопла, “не знают” о том, что происходит вне сопла (возмущения сносятся потоком частиц газа, и поток как бы запирает сопло).
течение внутри сопла перестает меняться, и расход также остается неизменным и равным критическому. Неизменность расхода объясняется тем, что слабые возмущения (а значит, и небольшие изменения противодавления) распространяются по частицам среды со скоростью звука. Поэтому при достижении критического режима (когда сами частицы на срезе сопла имеют скорость, равную скорости звука) частицы, находящиеся внутри сопла, “не знают” о том, что происходит вне сопла (возмущения сносятся потоком частиц газа, и поток как бы запирает сопло).
Замечание. Изменение противодавления 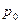 будет сказываться на течении газа вне сопла: в свободной струе вне сопла скорость при понижении
будет сказываться на течении газа вне сопла: в свободной струе вне сопла скорость при понижении 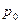 может стать сверхзвуковой, но поток в свободной струе не будет однородным (скорость в потоке существенно меняется по сечению струи).
может стать сверхзвуковой, но поток в свободной струе не будет однородным (скорость в потоке существенно меняется по сечению струи).

При истечении сжимаемого газа из тонкого отверстия скорость потока, как было показано выше, не может быть больше скорости звука. Достижение сверхзвуковой скорости истечения, как показали опыты Г. Лаваля (1845 – 1913), получается только при изменении конфигурации отверстия. В его экспериментах скорость истечения превышала скорость звука тогда, когда на выходе из сосуда устанавливалась специальная насадка, которая впоследствии была названа соплом Лаваля.
Сопло представляет собой короткий участок трубки переменного сечения с постепенным сужением, переходящим в расширение (рис. 7.20). Поток, попадая в узкое сечение, достигает минимальной скорости. С переходом в расширяющуюся часть трубки скорость растет, достигая сверхзвуковых значений. Такой характер изменения скорости газа при движении через сопло Лаваля можно обосновать, анализируя уравнение неразрывности сжимаемого газа и уравнение Эйлера для одномерного стационарного течения идеального газа.
 |
Уравнение неразрывности в трубке переменного сечения 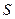 можно записать так:
можно записать так:
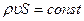 . (7.45)
. (7.45)
Уравнение Эйлера (для одномерного движения) имеет вид
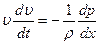 . (7.46)
. (7.46)
Дифференцируя (7.45) по координате 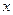 , имеем
, имеем
 (7.47)
(7.47)
Деля все члены (7.47) на 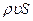 , получаем
, получаем
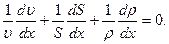 (7.48)
(7.48)
Считая течение адиабатическим и баротропным, из уравнения состояния находим
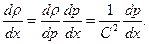
Тогда (7.48) можно переписать в виде
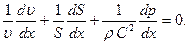
Подставляя сюда  из уравнения Эйлера (7.46), получим
из уравнения Эйлера (7.46), получим
 . (7.49)
. (7.49)
Уравнение (7.49) получено А. Гюгонио (1851 – 1887) и носит его имя. На основе (7.49) можно получить следующее заключение о характере изменения скорости в суживающихся и расширяющихся каналах.
При 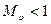 , изменение скорости
, изменение скорости 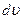 и сечения
и сечения 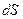 имеют разные знаки. Если сечение уменьшается, скорость увеличивается. Когда сечение увеличивается, скорость уменьшается. Такая картина хорошо известна и подтверждается в дозвуковых потоках.
имеют разные знаки. Если сечение уменьшается, скорость увеличивается. Когда сечение увеличивается, скорость уменьшается. Такая картина хорошо известна и подтверждается в дозвуковых потоках.
При 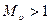 , скорость
, скорость 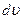 и сечение
и сечение 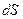 изменяются с одинаковым знаком. Если площадь сечения увеличивается, то скорость потока увеличивается. Когда сечение уменьшается, то скорость также уменьшается.
изменяются с одинаковым знаком. Если площадь сечения увеличивается, то скорость потока увеличивается. Когда сечение уменьшается, то скорость также уменьшается.
Такая ситуация при числах Маха, больших единицы, когда течение сверхзвуковое, представляется на первый взгляд парадоксальным. Однако такое несоответствие с реальностью устраняется благодаря тому, что при расширении газа его плотность уменьшается настолько заметно, что произведение плотности на площадь сечения, несмотря на рост площади, все же уменьшается, что и приводит к росту скорости с увеличением площади сечения. Следовательно, сверхзвуковой поток расширяется противоположно дозвуковому. Чтобы увеличить его скорость, трубку следует расширить.
При числах Маха, равных единице, скорость потока, равную скорости звука, можно получить только в минимальном сечении трубки. В максимальном сечении значение числа Маха, равное единице, не достигается, поскольку при расширении сечения скорость в дозвуковом потоке падает, а в сверхзвуковом – растет. Поэтому скорость течения, равную скорости звука, в наибольшем сечении получить невозможно. Таким образом, для получения в сопле скоростей течения газа, превышающих сверхзвуковые значения, сопло следует сначала сузить для достижения звуковой скорости, а затем расширить для дальнейшего увеличения скорости выходящего из него газа.
Результаты исследований законов сверхзвуковых течений газа в трубах переменного сечения оказали существенное влияние на развитие ракетной техники и космонавтики, а также лежат в основе конструкции аэродинамических труб, используемых для испытания сверхзвуковых летательных аппаратов.
 2014-02-02
2014-02-02 7624
7624
