Основные определения комбинаторного анализа

Лекция 2. Комбинаторика

В задачах комбинаторного анализа исследуются дискретные множества, т.е. множества, составленные из отдельных обособленных элементов. Особенность комбинаторных задач заключается в том, что в них внимание уделяется двум видам операций: отбору подмножеств и упорядочению элементов.

Выполнение комбинаторных операций отбора подмножеств осуществляется по двум логическим правилам:

1. Правило суммы. Если некоторый объект A можно выбрать n способами, а другой объект B можно выбрать m способами, то выбор либо A, либо B можно получить n+m способами.

2. Правило произведения. Если некоторый выбор A можно осуществить n различными способами, а для каждого этих способов некоторый другой выбор В можно осуществить m способами, то выбор А и В в указанном порядке можно осуществить 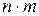способами.

Пример. В розыгрыше первенства страны по футболу принимают участие 16 команд. Сколькими способами могут быть распределены золотая и серебряная медали?

Решение. Золотую медаль может получить одна из 16 команд. После того как определен владелец золотой медали, серебряную медаль может получить одна из оставшихся 15 команд. Следовательно, общее число способов которыми могут быть распределены золотая и серебряная медали равно 16*15=240.

Рассмотрим множество A={a₁,…,a_n}.

Определение. Набор элементов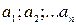называется выборкой объема r из n элементов или (n,r) - выборкой.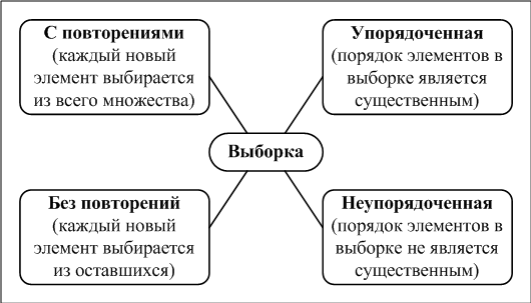

Если элементы упорядоченной (n;r) – выборки попарно различны, то такая выборка называется (n;r) – перестановкой. Число (n;r) – перестановок обозначается символом Р_n,r или P(n;r).

Упорядоченная (n;r) – выборка, в которой элементы могут повторяться, называется перестановкой с повторениями из n элементов по r и обозначается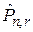или .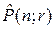

Упорядоченные перестановки в случае r<n называются размещениями из n элементов по r и обозначаются .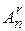

Неупорядоченная (n,r) - выборка без повторений называется сочетанием из n элементов по r и обозначаются.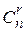

Неупорядоченная (n,r) -выборка с повторениями называется сочетанием с повторениями из n элементов по r и обозначаются.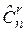

Пример. Пусть 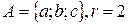. Указать все упорядоченные,неупорядоченные выборки с повторениями и без повторений из трех элементов по два.

Решение. 1. aa; ab; ac; ba; bb; bc; ca; cb; cc – девять перестановок с повторениями, .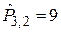

2. ab; ac; ba; bc; ca; cb – шесть перестановок без повторений, Р_3,2=6.

3. ab; ac; bc –три сочетания без повторений, .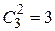

4. aa; ab; ac; bb; bc; cc – шесть сочетаний с повторениями, .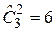

Теорема 1. Число упорядоченных r – элементных подмножеств множества А, состоящего из n элементов, равно .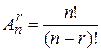

Следствие. Число (n;r) –размещений с повторениями равно .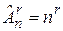

Пример. В классе изучают 10 предметов. В понедельник 6 уроков, причем все уроки различные. Сколькими способами можно составить расписание на понедельник?

Решение. Речь идет о 6 перестановках без повторения из 10 элементов. Тогда число способов составления расписания будет .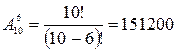

Пример. Для запирания сейфов и автоматических камер хранения применяют секретные замки, которые открываются лишь тогда, когда набрано «тайное слово». Это слово выбирают с помощью одного или нескольких дисков, на которых нанесены буквы. Пусть на диск нанесены 12 букв, а секретное слово из 5 букв. Сколько неудачных попыток может быть сделано человеком не знающим секретного слова?

Решение. Общее число комбинаций равно.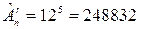

Теорема 2. Число перестановок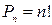

Следствие. Число перестановок, которые можно составить из 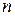элементов, среди которых имеется 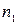элементов первого типа, 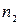элементов второго типа и т.д. равно .

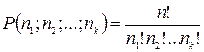Пример. Пакет акций состоит из акций четырех типов: 5 акций типа A, 3 акции типа B и по одной акции типов C и D. Сколькими способами можно распродать этот пакет, продавая по одной акции ежедневно?

Решение. Каждая распродажа однозначно определяется словом длины 10, составленном из пяти букв A, трех букв B, одной буквы C и одной буквы D (буква, стоящая на месте i, означает, что в день i была продана акция соответствующего типа). Значит, число всевозможных распродаж составляет .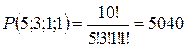

Теорема 3. Число всех неупорядоченных r – элементных подмножеств множества А, состоящего из n элементов, равно .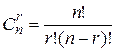

Следствие. Число (n;r) – сочетаний с повторениями равно .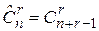

Пример. Найдем число способов разложить 10 одинаковых монет по трем карманам.

Решение. Каждый расклад монет представляет собой сочетание с повторениями из трех элементов по 10. Каждый «карман» входит в выборку столько раз, сколько монет в него положено. Таким образом, искомое число способов расклада равно

.

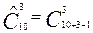Числа сочетаний 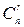присутствуют в формуле бинома Ньютона, откуда они получили название биномиальных коэффициентов.

Теорема 4. .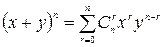

Доказательство. Эту формулу докажем методом математической индукции. База индукции: проверим при n =1

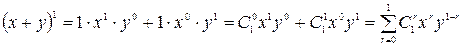, т.е. формула верна.

Индуктивное предположение. Предположим, что формула () верна для: n=k −1:

.

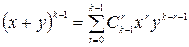Шаг индукции. Необходимо доказать, что формула верна для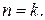

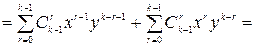
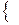распишем суммы

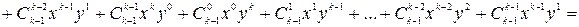{приведем подобные}=

=

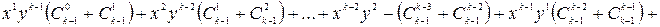
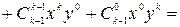{по свойству }=

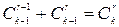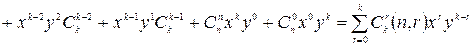. Теорема доказана.

Следствие 1. .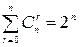

Следствие 2. .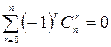

Теорема 5. .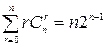

Теорема 6. .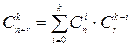

Из 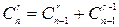следует способ вычисления биномиальных коэффициентов, известный как треугольник Паскаля.

1 1

1 2 1

1 3 3 1

1 4 6 4 1

В этом треугольнике каждое число (кроме единиц на боковых сторонах) является суммой двух чисел, стоящих над ним. Число сочетаний 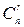находится в (n+1) -м ряду на (r+1) -м месте.