1. Производящая функция для (n;r) – сочетаний с ограниченным числом повторений
В этом случае для получения производящей функции нельзя воспользоваться формулой 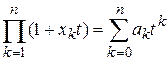 , поскольку всякий такой бином отражает лишь две возможности: элемент xk множества либо не появляется в r – сочетании, либо появляется ровно один раз. Пусть элемент xk появляется в r – сочетании с повторениями 0;1;2;…;j раз, тогда точно i появлениям элемента xk будет соответствовать одночлен
, поскольку всякий такой бином отражает лишь две возможности: элемент xk множества либо не появляется в r – сочетании, либо появляется ровно один раз. Пусть элемент xk появляется в r – сочетании с повторениями 0;1;2;…;j раз, тогда точно i появлениям элемента xk будет соответствовать одночлен 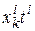 , а по правилу суммы появлению элемента xk либо 0, либо 1, …, либо j раз должен соответствовать многочлен
, а по правилу суммы появлению элемента xk либо 0, либо 1, …, либо j раз должен соответствовать многочлен 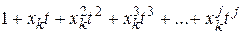 . Тогда производящая функция имеет вид
. Тогда производящая функция имеет вид  (
(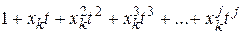 ). (7)
). (7)
Если надо найти лишь число  соответствующих
соответствующих 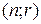 - сочетаний, то необходимо положить x1=x2=…=xj=1 и
- сочетаний, то необходимо положить x1=x2=…=xj=1 и  . (8)
. (8)
Коэффициенты 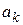 будут равны числу сочетаний из n элементов по k с j повторениями.
будут равны числу сочетаний из n элементов по k с j повторениями.
Пример. Рассмотрим сочетания из трех предметов 1;2;3, причем 1 и 2 могут встречаться не более двух раз, а 3 – не более одного раза.
Решение. Составим производящую функцию по формуле (7):
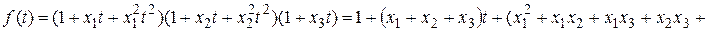
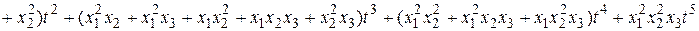 Если положить x1=x2=x3=1, то получим
Если положить x1=x2=x3=1, то получим 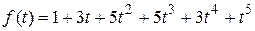 . Если не приравнивать то, коэффициент при t3 показывает состав r – сочетаний с указанными повторениями: 112;113;122;123;223. Коэффициент при t5 - число r – сочетаний из трех элементов по пять с повторениями: 11223.
. Если не приравнивать то, коэффициент при t3 показывает состав r – сочетаний с указанными повторениями: 112;113;122;123;223. Коэффициент при t5 - число r – сочетаний из трех элементов по пять с повторениями: 11223.
2. Производящая функция для (n;r) – сочетаний с неограниченным числом повторений
Найдем производящую функцию для (n;r) – сочетаний с условием, что хотя бы один элемент каждого вида появится в выборке. Очевидно, что 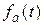 будет иметь вид
будет иметь вид  . (9)
. (9)
Сделаем замену индекса суммирования n+k=r, тогда получим
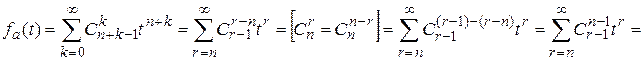
 .
.
Здесь 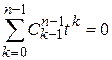 , следовательно число искомых r – сочетаний равно нулю при
, следовательно число искомых r – сочетаний равно нулю при 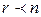 и
и 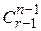 при
при 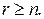
 2014-02-09
2014-02-09 1949
1949








