Логическая сущность метода включения и исключения определяется тем, что он применяется к задаче разделения множеств на подмножества в зависимости от того, обладают ли их элементы определенной совокупностью свойств или нет.
Пусть дано n- множество 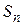 некоторых элементов и к-множество свойств
некоторых элементов и к-множество свойств 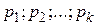 , которыми элементы
, которыми элементы 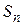 могут как обладать, так и не обладать. выделим какую-либо r-выборку свойств
могут как обладать, так и не обладать. выделим какую-либо r-выборку свойств 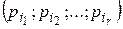 . Число элементов
. Число элементов 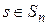 обладающих всеми r выбранными свойствами, обозначим через
обладающих всеми r выбранными свойствами, обозначим через 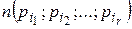 . Отсутствие у элемента какого-либо свойства
. Отсутствие у элемента какого-либо свойства 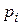 будем обозначать
будем обозначать 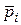 .
.
Найдем число элементов, не обладающих набором определенных свойств, начав с простых случаев:
1. Пусть имеется одно свойство 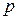 , тогда
, тогда 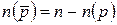 .
.
2. Имеется конечное число свойств 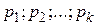 , несовместимых друг с другом. Тогда
, несовместимых друг с другом. Тогда 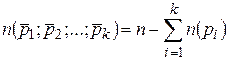 .
.
3. Элементы обладают комбинациями различных свойств. Тогда справедлива теорема.
Теорема3. Если даны n- множество элементов и к-множество свойств 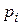 ,
, 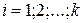 , совместимых между собой, тогда
, совместимых между собой, тогда
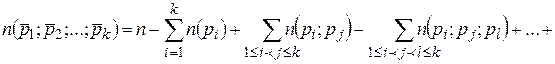
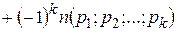 (20)
(20)
В левой части формулы может стоять не только 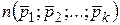 , но и, например,
, но и, например, 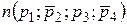 . Теорема формулируется при этом относительно совокупности свойств
. Теорема формулируется при этом относительно совокупности свойств 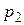 и
и 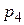 с обязательным выполнением свойств
с обязательным выполнением свойств 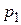 и
и 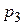 следующим образом:
следующим образом:
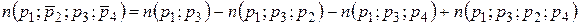 (21)
(21)
Пример. В комнате несколько человек, знающих хотя бы один из трех языков. Шестеро знают английский, шестеро – немецкий, семеро – французский. Четверо знают английский и немецкий, трое – немецкий и французский, двое – французский и английский. Один человек знает все три языка. Сколько человек в комнате. сколько из них знают только английский язык.
Решение. Пусть свойство 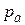 - знать английский язык;
- знать английский язык; 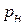 и
и 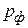 - свойства, характеризующие знание немецкого и французского языков. По условию задачи общее число людей составляют все, знающие хотя бы один язык; не знающих хотя один язык в задаче нет. Тогда
- свойства, характеризующие знание немецкого и французского языков. По условию задачи общее число людей составляют все, знающие хотя бы один язык; не знающих хотя один язык в задаче нет. Тогда
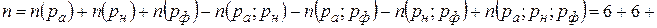
+7-(4+3+2)+1=19-9+1=11.
Число людей, знающих только английский язык, это 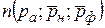 , по формуле (21) имеем
, по формуле (21) имеем
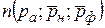 =
=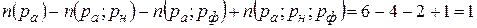 .
.
 2014-02-09
2014-02-09 2599
2599








