Дифференциальные уравнения цепи с распределенными параметрами

Рассмотрим двухпроводную однородную линию, физические параметры которой равномерно распределены по ее длине:

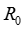― активное сопротивление пары проводов на единицу длины [Ом/м], определяется по известной формуле 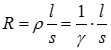, зависит от материала провода (γ) и от ее температуры ;

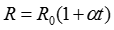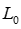― индуктивность пары проводов на единицу длины линии [Гн/м], определяется как отношение потокосцеплепия к току (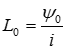), является отображением магнитного поля линии в ее схеме замещения, зависит от магнитных характеристик среды (μ) и геометрических размеров линии;

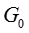― активная проводимость между проводами на единицу длины линии [См/м], является следствием несовершенства изоляции между проводами, зависит от электрических параметров среды (γ) и геометрических размеров линии;

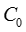― емкость между проводами на единицу длины линии [Ф/м], определяется как отношение заряда к напряжению(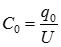), является отображением электрического поля линии в ее схеме замещения, зависит от электрических характеристик среды (e) и геометрических размеров линии.

Удельные параметры линии 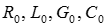зависят от физических параметров самих проводов и окружающий их среды, поэтому они получили название физических или первичных.

Разделим всю линию на элементарные участки длиной dх и рассмотрим один из таких участков, находящийся на расстоянии х от начала линии. Схема замещения участка будет иметь вид рис.1.Здесь u и i ― напряжение и ток в начале рассматриваемого участка. В конце участка напряжение и ток получают приращения: 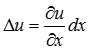и .

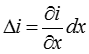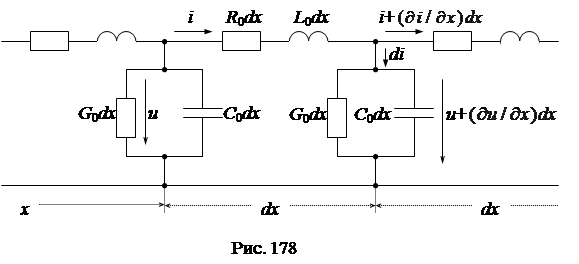Функции напряжения и тока (u, i) зависят от двух параметров t и x, они изменяются в пространстве и во времени, поэтому дифференциальные уравнения для схемы замещения следует составлять в частных производных.

Уравнение по 2-му закону Кирхгофа для контура:

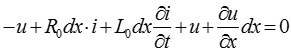После упрощения получим:

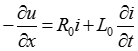(1).

По закону Ома и 1-му закону Кирхгофа:

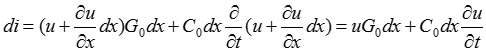
В приведенном выражении пренебрегаем слагаемыми второго порядка малости, содержащими .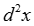

По 1-му закону Кирхгофа для узла:

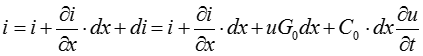
После упрощения получим:

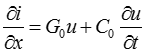- (2).

Уравнения (1) и (2) являются основными дифференциальными уравнениями двухпроводной линии с распределенными параметрами, которые используются для расчета как переходного, так и установившегося режима линии.

3. Решение уравнений линии с распределенными параметрами в установившемся синусоидальном режиме

Пусть напряжение и ток в линии с распределенными параметрами изменяются по синусоидальному закону:

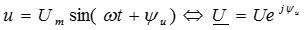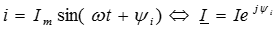Заменим в дифференциальных уравнениях линии синусоидальные функци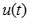и и 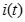и их производные 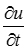и 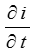соответствующими комплексными изображениями , , , :

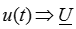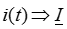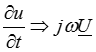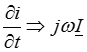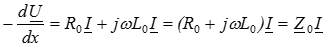(1)

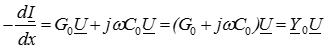(2)

В уравнениях (1) и (2) приняты обозначения: 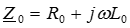- комплексное сопротивление линии на единицу длины [Ом /м], 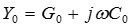- комплексная проводимость линии на единицу длины [См /м].

Дифференцируем уравнение (2) по переменной х и делаем в него подстановку из (1):

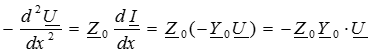или

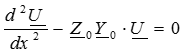(3)

Решаем дифференциальное уравнение 2-го порядка (3) классическим методом. Характеристическое уравнение и его корни:

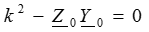, откуда --, ++.

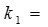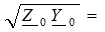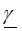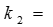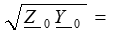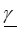Решение для искомой функции в общем виде:

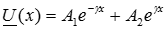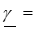
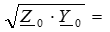
где 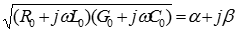- безразмерная комплексная величина, названная коэффициентом (постоянной) распространения, 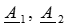- комплексные постоянные интегрирования, которые определяются через граничные условия, т. е. через значения искомых функций U (x), I (x) в заданной точке линии, например в ее начале (х =0) или в ее конце (x = l).

Из уравнения (1) находим:

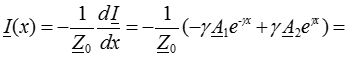
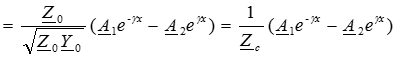
где 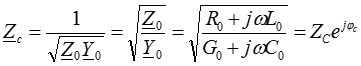― волновое или характеристическое сопротивление линии.

Таким образом, решения для искомых функций U (x) и I (x) имеют вид:

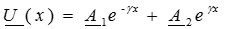, (4)

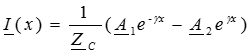. (5)

Волновое сопротивление 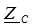и постоянная распространения 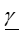получили название вторичных параметров линии.

Выразим постоянные интегрирования 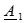и 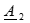через граничные условия начала линии. При х =0 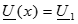, , 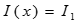подставим эти значения в уравнения (4) и (5):

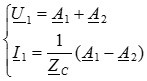
Совместное решение этих уравнений позволяет определить постоянные интегрирования:, .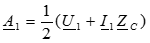

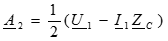Подставим полученные значения постоянных интегрирования в решения для искомых функций (4) и (5):

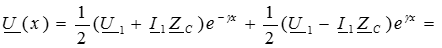
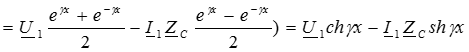
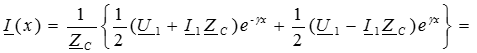
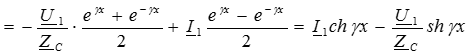
Полученные уравнения используются при расчетах цепей с распределенными параметрами в установившемся синусоидальном режиме.

Если принять х = l,то получим значения параметров режима в конце линии:

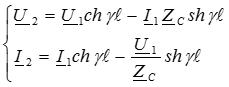
Выразим постоянные интегрирования через граничные условия конца линии. Для этой цели в полученных ранее решениях (4) и (5) заменим переменные х на l-y из условия x=l-y, где l ― длина всей линии, а y ― расстояние от конца линии до рассматриваемой точки:

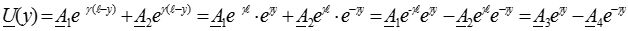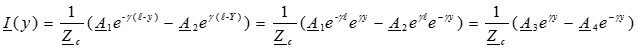Здесь 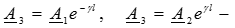есть некоторые новые постоянные интегрирования.

При y =0 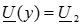, 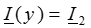подставим эти значения в найденные уравнения, получим:

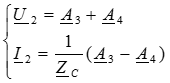
Совместное решение этих уравнений позволяет определить постоянные интегрирования:

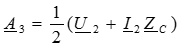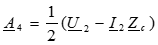
Подставляем значение постоянных в решение для искомых функций:

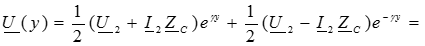
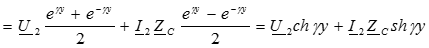
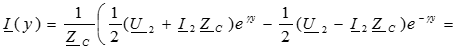
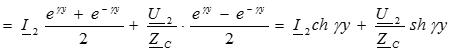
Полученные уравнения используются при расчете цепей с распределенными параметрами в установившемся синусоидальном режиме.

Если принять y = l, то получим значение параметров режима в начале линии:

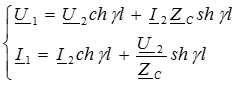
Волновые процессы в линии с распределенными параметрами.

Ранее были получены решения для напряжения и тока в установившемся режиме:

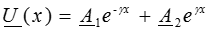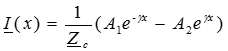Учитывая, что постоянные интегрирования и коэффициент распространения являются комплексными числами (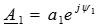, , 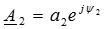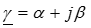) преобразуем уравнение для U (x):

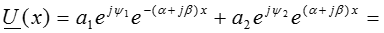
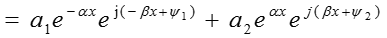Перейдем от комплексного изображения функции к ее оригиналу, т.е. к ее функции времени:

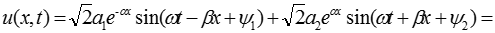
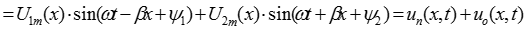Функция u (x,t) состоит из двух слагаемых, первое из которых представляет собой прямую или падающую волну u_п (x,t), а второе - обратную или отраженную волну u_о (x,t). Проанализируем, как изменяется каждая из волн в пространстве и во времени.

Падающая волна напряжения равна: .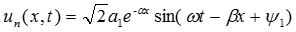

В произвольной точке линии 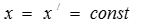напряжение изменяется по синусоидальному закону с постоянной амплитудой:

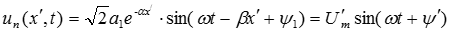где , .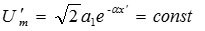

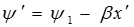В произвольно выбранный момент времени 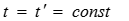напряжение вдоль линии изменяется по синусоидальному закону, но с затуханием амплитуды с увеличением расстояния х:

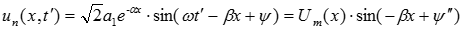где , .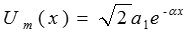

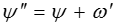Коэффициент β показывает, как изменяется фаза падающей волны напряжения на единицу длины линии [рад/м] и называется коэффициентом фазы.

Длиной волны λ называется расстояние ∆ х между двумя ближайшими точками линии, которые находятся в одинаковом фазовом состоянии, т.е. через интервал 2 π:

β ∆ x = βλ = 2 π, откуда следует .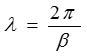

С течением времени синусоидальное распределение напряжения перемещается вдоль линии. Под скоростью распространения волны или фазовой скоростью понимают скорость перемещения вдоль линии определенного фазового состояния, для чего должно удовлетворяться условие: .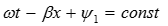

Продифференцируем члены этого уравнения, в результате получим: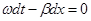, откуда следует:

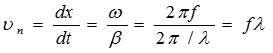
Неравенство 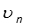> 0 означает, что падающая волна перемещается в положительном в направлении, т. е. от начала линии к ее концу.

Амплитуда падающей волны зависит от координаты х: 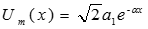, она

убывает (затухает) по показательному закону 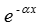в направление возрастания х, т.е. в направлении движения волны. Скорость затухания определяется коэффициентом α, который получил название коэффициента затухания волны [Неп/м].

Коэффициент 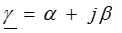показывает в комплексе характер изменения волны при движении ее вдоль линии, поэтому получил название коэффициента распространения волны.

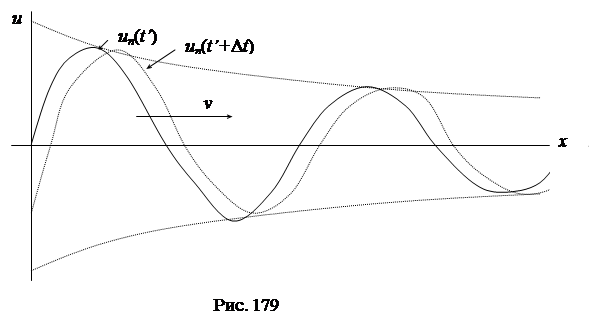
Характер распространения падающей волны напряжения показан на рис. 179.

Отраженная волна напряжения равна:

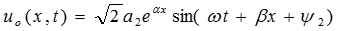Фазовая скорость отраженной волны найдется из уравнения: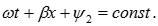

После дифференцирования получим: 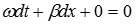, откуда следует

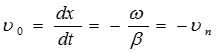
Отраженная волна распространяется с той же фазовой скоростью, что и падающая, но в обратном направлении(знак минус), т.е. от конца линии к ее началу. Она имеет ту же длину волны 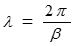. Амплитуда отраженной волны 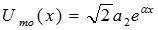, при α > 0 убывает (затухает) в направлении уменьшения координаты х, т.е. в направлении движения волны.

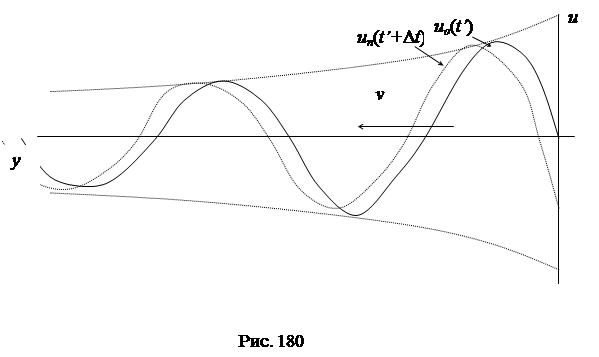
Характер распространения отраженной волны показан на рис. 180.

Действительное значение напряжения в любой точке лини х’ в любой момент времени t’ будет равно сумме значений напряжений падающей и отражённой волн:

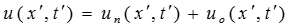Очевидно, что функцию тока в линии 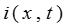также можно рассматривать как результат наложение падающей 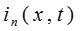и отражённой 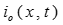волн стой лишь разницей, что отражённая волна накладывается с обратным знаком:

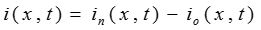5. Линия с распределенными параметрами в различных режимах

Расчет токов и напряжений в линии с распределенными параметрами при произвольной нагрузке 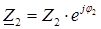на основе совместного решения полученных ранее комплексных уравнений. Уравнения режима линии дополняются уравнениями закона Ома для начала и конца линии:

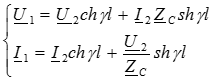
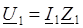
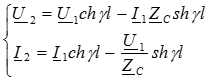
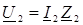
где Z ₁- входное сопротивление линии при заданной нагрузке:

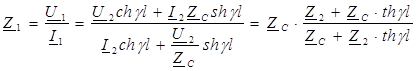
Выбор алгоритма расчета определяется конкретными условиями задачи. Рассмотрим характерные режимы линии, представляющие теоретический интерес.

1. Режим холостого хода .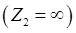

В режиме холостого хода 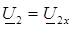; 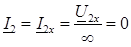, следовательно уравнения линии получат укороченный вид:

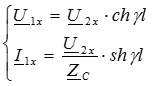
Входное сопротивление линии в режиме холостого хода:

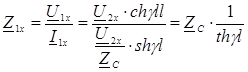2. Режим короткого замыкания .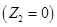

В режиме короткого замыкания 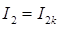,,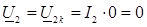 следовательно уравнения линии получат указанный вид:

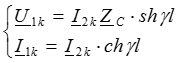
Входное сопротивление линии в режиме короткого замыкания:

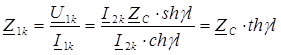Совместно выполненные опыты холостого хода и короткого замыкания позволяют экспериментально определить сначала вторичные параметры лини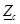и (и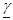), а затем и первичные (R ₀, L ₀, G ₀, C ₀).

Входные сопротивления лини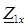и и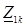экспериментально измеряются по схеме трех приборов (амперметра, вольтметра и фазометра), как .

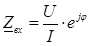Вторичные параметры линии (Z _C и g) находятся из совместного решения уравнений для 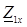и: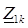

;

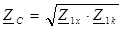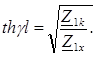
Первичные параметры линии (R ₀, L ₀, G ₀, C ₀) определяются из совместного решения уравнений для 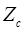и: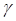

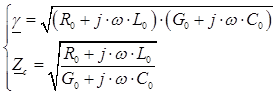Решая совместно эти уравнения, получим:

, .

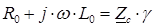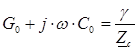3. Режим согласованной нагр узки .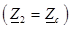

В режиме согласованной нагрузки входное сопротивление линии равно:

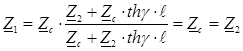Исследуем волновые процессы в линии:

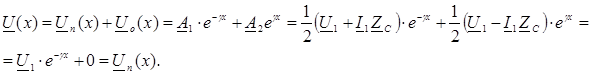
В режиме согласованной нагрузки в линии отсутствуют отраженные волны напряжения и тока. Вся энергия, доставляемая падающей волной в конец линии полностью потребляется нагрузкой, при этом передаваемая приемнику активная мощность имеет максимальное значение:

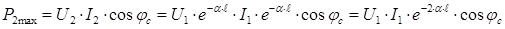Мощность источника энергии: .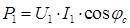

Коэффициент полезного действия: .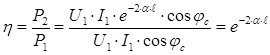

Если сопротивление нагрузки несогласованно с волновым сопротивлением линии 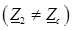, то часть энергии, доставляемой падающей волной, отражается и возвращается генератору в виде отраженных волн напряжения и тока.

В линиях связи отраженные волны ухудшают качество основного сигнала (снижается разборчивость речи, четкость изображения и др.). Все линии связи работают в режиме, близком к согласованному. При различии сопротивлений нагрузки и линии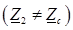принимаются специальные технические меры для их согласования.