Выделим произвольную точку n, расположенную в электростатическом поле на поверхности раздела двух диалектриков с разными значениями диэлектрической проницаемости 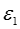 и
и  (рис. 3)
(рис. 3)
 |
Окружим точку n элементарной призмой, у которой высота бесконечно мала по сравнению с линейными размерами основания. Применим к поверхности призмы теорему Гаусса, при этом пренебрежем потоком вектора  через боковые поверхности ввиду их малости. Тогда получим:
через боковые поверхности ввиду их малости. Тогда получим:
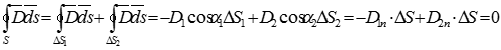 , или
, или
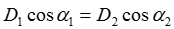 ,
, 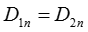 .
.
На границе раздела двух диэлектриков равны нормальные составляющие вектора электрического смещения 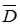 .
.
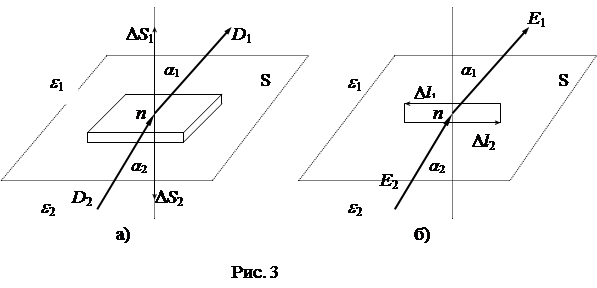
Окружим выделенную точку n элементарным прямоугольником, высота которого бесконечно мала по сравнению с его длиной (рис. 3б). Найдем значение циркуляции вектора 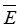 по периметру прямоугольника:
по периметру прямоугольника:
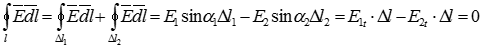 , или
, или
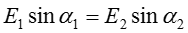 ,
, 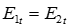 .
.
На границе раздела двух диэлектриков равны тангенциальные составляющие вектора напряженности поля 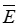 .
.
Разделим почленно вторые уравнения на первые и учтем, что 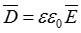 , получим
, получим
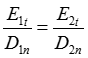 или
или 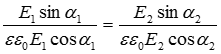 , откуда следует
, откуда следует
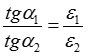 ― условие преломления линий поля на поверхности раздела двух диэлектриков с различными значениями и диэлектрической проницаемости(
― условие преломления линий поля на поверхности раздела двух диэлектриков с различными значениями и диэлектрической проницаемости(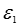 и
и 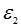 ).
).
Если линии поля направлены нормально к поверхности раздела (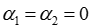 ), то
), то
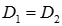 ,
, 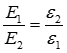 .
.
Рассмотрим граничные условия на поверхности раздела диэлектрика с проводником.
Электрическое поле внутри проводника отсутствует (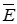 = 0), а его поверхность является эквипотенциальной. На поверхности проводника бесконечно тонким слоем будут располагаться свободные разряды с поверхностной плотностью
= 0), а его поверхность является эквипотенциальной. На поверхности проводника бесконечно тонким слоем будут располагаться свободные разряды с поверхностной плотностью 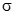 . Лини поля в диэлектрике будут направлены нормально к поверхности проводника как к эквипотенциальной поверхности. Применяя рассуждения, аналогичные предыдущему примеру, получим:
. Лини поля в диэлектрике будут направлены нормально к поверхности проводника как к эквипотенциальной поверхности. Применяя рассуждения, аналогичные предыдущему примеру, получим:
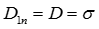 ,
, 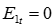 .
.
 2014-02-09
2014-02-09 3097
3097








