Транспортная задача
Задача линейного программирования (симплекс-метод)
Задача распределения ресурса на сетях
Задача определения продолжительности проекта
Задачи календарно-сетевого планирования и управления
Потоковые задачи
Путь максимальной эффективности с учетом штрафов.
Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
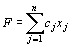 (8)
(8)
при условиях
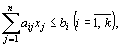 (9)
(9)
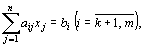 (10)
(10)
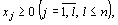 (11)
(11)
где 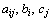 - заданные постоянные величины и
- заданные постоянные величины и 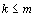 .
.
Функция (8) называется целевой функцией (или линейной формой) задачи (8) – (11), а условия (9) – (11) – ограничениями данной задачи.
Стандартной (или симметричной} задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (9) и (11), где k = m и l = n.
Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (10) и (11), где k = 0 и l = п.
Совокупность чисел 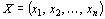 ,удовлетворяющих ограничениям задачи (9) – (11), называется допустимым решением (или планом).
,удовлетворяющих ограничениям задачи (9) – (11), называется допустимым решением (или планом).
План 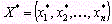 , при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.
, при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.
Значение целевой функции (8) при плане Х будем обозначать через 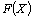 . Следовательно, X* – оптимальный план задачи, если для любого Х выполняется неравенство
. Следовательно, X* – оптимальный план задачи, если для любого Х выполняется неравенство 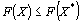 [соответственно
[соответственно 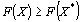 ].
].
Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач.
Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно уметь, во-первых, сводить задачу минимизации функции к задаче максимизации; во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот; в-третьих, заменять переменные, которые не подчинены условию неотрицательности.
8.4.1.Симплекс –метод решения ЗЛП, реализация симплекс-метода с помощью таблиц
Симплекс-метод – это аналитический метод решения основной задачи линейного программирования. Пусть требуется максимизировать линейную функцию L=c1x1+ c2x2+…+ cnxn+c0 при условиях 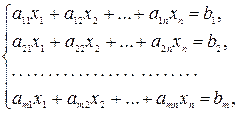 (1)
(1)
где x1, x2,…, xn≥0.
Выразим x1, x2,…, xr (r≤m) через остальные переменные:
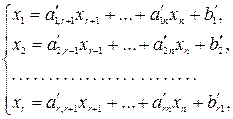 (2)
(2)
где b'1 ≥ 0, b'2 ≥ 0, …, b'r ≥ 0.
Переменные x1, x2,…, xr называются базисными, а весь набор { x1, x2,…, xr } - базисом, остальные переменные называются свободными, система ограничений (2)называется системой, приведенной к единичному базису. Подставляя в линейную форму L вместо базисных переменных их выражения через свободные переменные из системы (2), получим L=γ0+ γr+1 xr+1+…+ γn xn.
Теперь, полагая все свободные переменные равными нулю, найдем значения базисных переменных: x1= b'1, x2= b'2, …, xr= b'r. Таким образом, решение (b'1, b'2, …, b'r, 0, …, 0) системы является допустимым - оно называется базисным. Для полученного базисного решения значение линейной формы LБ=γ0. Решение задачи при помощи симплекс-метода распадается на ряд шагов, заключающихся в том, что от данного базиса Б мы переходим к другому базису Б' с таким расчетом, чтобы значение LБ увеличивалось или, по крайней мере, не уменьшалось, т.е. LБ' ≥ LБ.
Замечание. 1. Если ограничительные условия заданы неравенствами, то их можно преобразовать в равенства путем введения новых неотрицательных переменных - так называемых балансовых (выравнивающих). Так, например, в неравенстве a1x1+ a2x2+…+ anxn≤b достаточно добавить в левую часть некоторую величину xn+1≥0 и получится равенство a1x1+ a2x2+…+ anxn+ xn+1=b.
2. Если переменная xl не подчинена условию неотрицательности, то её заменяют разностью двух неотрицательных переменных: xl = ul- vl, где ul, vl≥0.
3. Задача минимизации функции L сводится к задаче максимизации функции ‑ L.
Симплекс-метод обычно реализуют с помощью симплекс-таблиц. Сведем систему ограничений к единичному базису:
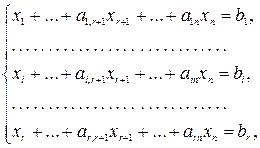
а линейную форму L - к виду L+ γr+1 xr+1+…+ γj xj +…+ γn xn=γ0. (3)
В виде таблицы эти данные можно представить так:
| Базисные переменные | Свободные члены | x1 | … | xi | … | xr | xr+1 | … | xj | … | xn |
| x1 | b1 | … | … | a1,r+1 | … | A1j | … | a1n | |||
| … | … | … | … | … | … | … | … | … | … | … | … |
| xi | bi | … | … | ai,r+1 | … | aij | … | ain | |||
| … | … | … | … | … | … | … | … | … | … | … | … |
| xr | br | … | … | ar,r+1 | … | arj | … | arn | |||
| L | γ0 | … | … | γr+1 | … | γj | … | γn |
Равенство (3) будем называть приведенным (к свободным переменным) выражением для функции L, а коэффициенты γj - оценками (индексами) соответствующих свободных переменных xj.
1. Выбираем разрешающий столбец ap из условия: оценка γp<0 и хотя бы один элемент aip>0.
2. Выбираем q -ю разрешающую строку из условия bq / aqp=min{bi / aip} для aip>0.
3. Производим пересчет элементов разрешающей q -й строки по формуле a'qk = aqk / aqp (k=0,1,…,n).
4. Вычисляем элементы всех остальных строк (при k≠p) по формуле a'ik = aik - a'qk ∙ aip (i=0,1,…,q-1,q+1,…,r).
Следует иметь в виду следующую теорему, которую мы приводим без доказательства.
Теорема. Если после выполнения очередной итерации:
1. найдется хотя бы одна отрицательная оценка и в каждом столбце с такой оценкой окажется хотя бы один положительный элемент, т.е. γk<0 для некоторых k, и aik>0 для тех же k и некоторого i, то можно улучшить решение, выполнив следующую итерацию;
2. найдется хотя бы одна отрицательная оценка, столбец которой не содержит положительных элементов, т.е. γk<0, aik<0 для какого-то k и всех i, то функция L не ограничена в области допустимых решений (Lmax→ ∞);
3. все оценки окажутся неотрицательными, т.е. γk≥0 для всех k, то достигнуто оптимальное решение.
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из т пунктов отправления  в п пунктов назначения
в п пунктов назначения  . При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через
. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через 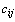 тарифы перевозки единицы груза из i -го пункта отправления в j -й пункт назначения, через
тарифы перевозки единицы груза из i -го пункта отправления в j -й пункт назначения, через 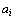 – запасы груза в i -м пункте отправления, через
– запасы груза в i -м пункте отправления, через 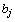 – потребности в грузе в j– м пункте назначения, а через
– потребности в грузе в j– м пункте назначения, а через 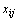 – количество единиц груза, перевозимого из i -го пункта отправления в j -й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции
– количество единиц груза, перевозимого из i -го пункта отправления в j -й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции
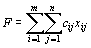 (63)
(63)
при условиях
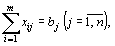 (64)
(64)
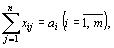 (65)
(65)
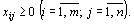 (66)
(66)
Поскольку переменные 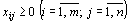 удовлетворяют системам линейных уравнений (64) и (65) и условию неотрицательности (66), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.
удовлетворяют системам линейных уравнений (64) и (65) и условию неотрицательности (66), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.
Всякое неотрицательное решение систем линейных уравнений (64) и (65), определяемое матрицей 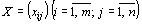 , называется планом транспортной задачи.
, называется планом транспортной задачи.
План 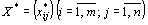 , при котором функция (63) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
, при котором функция (63) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
Обычно исходные данные транспортной задачи записывают в виде таблицы (см. табл. 8.1).
Таблица 8.1

Очевидно, общее наличие груза у поставщиков равно 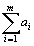 ,а общая потребность в грузе в пунктах назначения равна
,а общая потребность в грузе в пунктах назначения равна 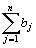 единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е.
единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е.
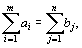 (67)
(67)
то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.
Теорема: Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. чтобы выполнялось равенство (67).
В случае превышения запаса над потребностью, т. е. 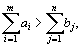 вводится фиктивный (n +1)–й пункт назначения с потребностью
вводится фиктивный (n +1)–й пункт назначения с потребностью 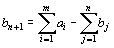 и соответствующие тарифы считаются равными нулю:
и соответствующие тарифы считаются равными нулю: 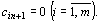 Полученная задача является транспортной задачей, для которой выполняется равенство (67).
Полученная задача является транспортной задачей, для которой выполняется равенство (67).
Аналогично, при 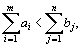 вводится фиктивный (m +1)–й пункт отправления с запасом груза
вводится фиктивный (m +1)–й пункт отправления с запасом груза 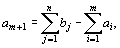 и тарифы полагаются равными нулю:
и тарифы полагаются равными нулю: 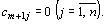 Этим задача сводится к обычной транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи. В дальнейшем будем рассматривать закрытую модель транспортной задачи. Если же модель конкретной задачи является открытой, то, исходя из сказанного выше, перепишем таблицу условий задачи так, чтобы выполнялось равенство (67).
Этим задача сводится к обычной транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи. В дальнейшем будем рассматривать закрытую модель транспортной задачи. Если же модель конкретной задачи является открытой, то, исходя из сказанного выше, перепишем таблицу условий задачи так, чтобы выполнялось равенство (67).
Число переменных 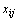 в транспортной задаче с т пунктами отправления и п пунктами назначения равно пт, а число уравнений в системах (64) и (65) равно п+т. Так как мы предполагаем, что выполняется условие (67), то число линейно независимых уравнений равно п+т– 1. Следовательно, опорный план транспортной задачи может иметь не более п + т– 1 отличных от нуля неизвестных.
в транспортной задаче с т пунктами отправления и п пунктами назначения равно пт, а число уравнений в системах (64) и (65) равно п+т. Так как мы предполагаем, что выполняется условие (67), то число линейно независимых уравнений равно п+т– 1. Следовательно, опорный план транспортной задачи может иметь не более п + т– 1 отличных от нуля неизвестных.
Если в опорном плане число отличных от нуля компонент равно в точности п+т– 1, то план является невырожденным, а если меньше – то вырожденным.
 2014-02-09
2014-02-09 752
752







