Рассмотрим таблицы истинности формул 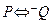 и
и 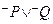 :
:
| Р | Q | 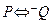
| 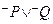
|
| И | И | Л | Л |
| И | Л | И | И |
| Л | И | И | И |
| Л | Л | Л | И |
Из таблиц видно, что при всех наборах значений P и Q, при которых формула 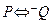 принимает значение «И», это же значение «И» принимает и формула
принимает значение «И», это же значение «И» принимает и формула 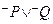 .
.
Определение. Из формулы А логически следует формула В, если по крайней мере при всех тех наборах значений атомов, входящих в А или В, при которых формула А имеет значение «И», формула В тоже имеет значение «И».
Логическое следование обозначают: А╞В.
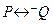 ╞
╞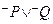
А╞В
Из формул 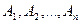 логически следует формула В (т.е.
логически следует формула В (т.е. 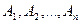 ╞В), если формула В имеет значение «И» по крайней мере при всех тех значениях атома, входящих в формулы
╞В), если формула В имеет значение «И» по крайней мере при всех тех значениях атома, входящих в формулы 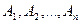 , при которых значение «И» имеют формулы
, при которых значение «И» имеют формулы 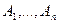 одновременно.
одновременно.
Th. 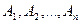 ╞В, тогда и только тогда, когда
╞В, тогда и только тогда, когда 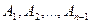 ╞
╞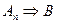 .
.
Это утверждение доказывается методом от противного.
 2014-02-09
2014-02-09 449
449







