Соединения элементов

Гармонические напряжение и ток в цепи последовательного

Пусть в цепи из последовательно соединённых сопротивления R, индуктивности 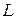и ёмкости 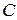(рис. 5.3) протекает гармонический ток

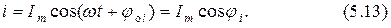
Рис. 5.3. Последовательное соединение 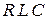элементов (а) и эквивалентная схема соединения (б)

По второму закону Кирхгофа с учётом выражений (2.1), (2.12) и (3.10) получаем уравнение цепи с последовательным соединением элементов

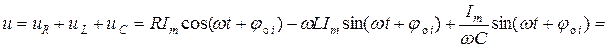
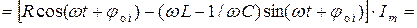
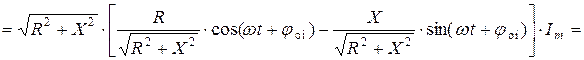
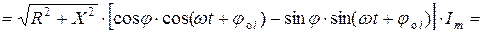
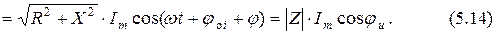
Здесь

– реактивная составляющая полного сопротивления цепи,

– модуль полного сопротивления цепи,

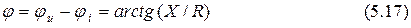
– фазовый сдвиг между напряжением на выводах цепи и током, протекающим в ней.

В зависимости от знака 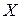фазовый сдвиг в цепи последовательного соединения 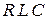может быть положительным, отрицательным или нулевым.

При положительном 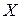эквивалентное сопротивление 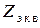можно представить в виде последовательного соединения резистора и некоторой эквивалентной индуктивности, величина которой равна

что следует из формулы (5.15).

При 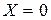имеет место соотношение

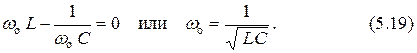
Величину 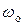называют резонансной частотой цепи последовательного соединения 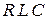элементов.

Если реактивная составляющая полного сопротивления отрицательная, то эквивалентное сопротивление 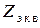будет представлять собой последовательное соединение резистора и некоторой эквивалентной ёмкости, величину которой можно рассчитать по формуле

Так как согласно формуле (5.15) 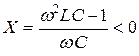, то 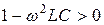и поэтому 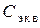положительная.