Плоскости

Представление гармонических функций на комплексной

Законы Кирхгофа в комплексной форме

Запись закона Ома в комплексной форме

Представление гармонических функций на комплексной плоскости

ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

ЛЕКЦИЯ 6

ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ К РАСЧЁТУ

План лекции:

Основным недостатком классического метода анализа линейных электрических цепей при гармоническом воздействии является громоздкость тригонометрических преобразований, что приводит к большой трудоёмкости и повышает вероятность появления ошибок.

Тригонометрическая форма представления гармонических функций времени удобна только в случае простейших электрических цепей. Для расчёта более сложных цепей был предложен метод комплексных амплитуд, введённый в инженерную практику в 1893-94 годах американскими учёными А.К. Кеннели и Ч.П. Штейнметцем.

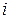В электротехнике и радиотехнике в отличие от математики для обозначения мнимой единицы используют символ , так как символом обозначают ток. На комплексной плоскости комплексное число 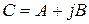может быть представлено вектором (рис. 6.1). В качестве положительного откладывают угол от действительной оси против часовой стрелки.

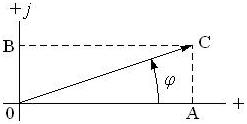
Рис. 6.1. Вектор , изображающий комплексное число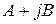

Возможны четыре формы записи комплексных чисел:

– алгебраическая

– показательная

– тригонометрическая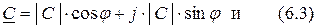

– полярная

Длина вектора 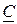(длина гипотенузы прямоугольного треугольника 0АС) может быть рассчитана по формуле 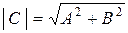. Её называют амплитудой комплексного числа. Отрезок представляет собой действительную, отрезок 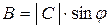– мнимую части комплексного числа, 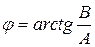– угол или фазу комплексного числа.

Тригонометрическая и алгебраическая формы записи удобны при сложении и вычитании комплексных чисел, показательная – при умножении и делении.

Найдем сумму двух комплексных чисел (рис. 6.2)

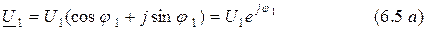
и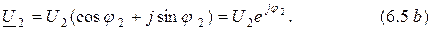

В тригонометрической форме записи имеем выражение

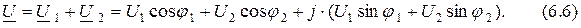
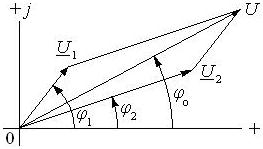
Рис. 6.2. Векторная диаграмма сложения двух комплексных величин

Найдём модуль 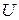и фазу 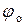этого комплексного числа (рис. 6.2):

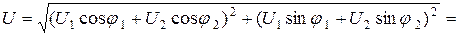
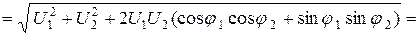
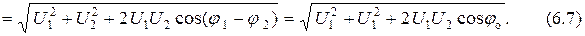
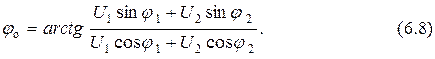
Поэтому в показательной форме выражение (6.6) может быть записано

как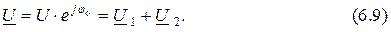

Следовательно, действительная и мнимая части результирующего комплексного числа 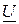могут быть представлены в виде:

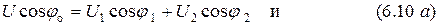
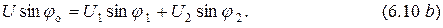
Переходя к гармоническим функциям, рассмотрим комплексное число

где 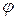– начальная фаза. При 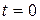вектор комплексного числа имеет вид, показанный на рис. 6.1. Вектор 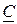, не изменяясь по величине, вращается против часовой стрелки с угловой частотой 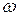. Поэтому множитель 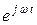называют оператором вращения.

Множитель 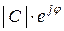, не зависящий от времени, называют комплексной амплитудой и обозначают символом с подчёркиванием или с точкой над ним

Проекция вектора 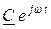на действительную ось представляет собой косинусоидальную функцию и является действительной частью комплексного выражения (6.1). Проекция этого же вектора на мнимую ось есть мнимая часть комплексного выражения (6.1).

Рассматривать вращающийся вектор неудобно. Поэтому положение вектора фиксируют, а оси координат считают вращающимися по часовой стрелке, что также неудобно.

Однако для сравнения векторов с одинаковыми частотами вращения достаточно знать их начальные положения, так как при вращении взаимное положение векторов не изменяется.

Диаграмму, изображающую совокупность векторов, имеющих одинаковую частоту вращения и построенных с соблюдением их взаимной ориентации по начальным фазам, называют векторной диаграммой.

Векторное представление гармонических функций с одинаковыми частотами облегчает операции сложения и вычитания.

Пусть, например, даны два комплексных числа

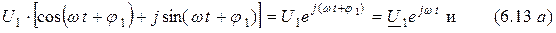
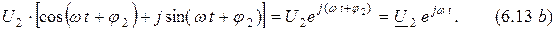
Найдём их сумму:

Сократив уравнение (6.14) на общий множитель 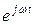(оператор вращения), делаем вывод, что векторную диаграмму для гармонических функций с одинаковыми частотами можно рассматривать как неподвижную и вести расчёты с комплексными амплитудами. Такой подход существенно упрощает работу, так как не требует громоздких тригонометрических преобразований. И только в конце расчёта при переходе к функциям времени нужно будет домножить комплексные амплитуды на оператор вращения и взять действительную часть комплексного числа.