ФИНАЛ
Чемпионата на «Кубок Москвы» Лиги колледжей
по игре «ИНТЕЛЛЕКТУАЛЬНОЕ ШОУ «ВОРОШИЛОВСКИЙ СТРЕЛОК»
| ЮАО «Крепкие орешки» колледж гостиничного хозяйства № 37 |
| 3 МЕСТО ЮАО «Инноваторы» Московский колледж управления и новых технологий |
| 2 МЕСТО ЮАО «Инноваторы» Московский колледж управления и новых технологий |
| 1 МЕСТО ЮАО «Кассиопея» Московский колледж управления и новых технологий |
| ЮАО «Кассиопея» Московский колледж управления и новых технологий |
| ЮЗАО «Фемида» Юридический колледж Российской академии правосудия |
| ЮАО «Кассиопея» Московский колледж управления и новых технологий |
| ВАО «МКАМ» Московский колледж авиа-мотостроения |
| САО «КП 11» Колледж предпринимательства № 11 |
| ЮЗАО «Фемида» Юридический колледж Российской академии правосудия |
| ЮАО «Инноваторы» Московский колледж управления и новых технологий |
| ВАО «Интеллектуалы» Колледж № 23 индустрии гостеприимства и менеджмента |
| ВАО «Интеллектуалы» Колледж № 23 индустрии гостеприимства и менеджмента |
| ЮАО «Титаны» Колледж сферы услуг №32 |
| ЮАО «Титаны» Колледж сферы услуг №32 |
| ЮАО «Крепкие орешки» колледж гостиничного хозяйства № 37 |
| ЮАО «Инноваторы» Московский колледж управления и новых технологий |
| ЮАО «Кассиопея» Московский колледж управления и новых технологий |
| ЗАО «Луч» Строительный колледж № 41 |
| ВАО «МКАМ» Московский колледж авиа-мотостроения |
| САО «КП 11» Колледж предпринимательства № 11 |
| САО «Королевичи» Колледж автомобильного транспорта №9 |
| ЮАО «Почти юристы» Юридический колледж |
| ЮАО «Титаны» Колледж сферы услуг №32 |
| САО «Налоговики» Налоговый колледж |
| ВАО «Пчёлки» Московский автомобильно-дорожный колледж им Николаева |
| ЮЗАО «Лекс ЭЮК» Экономико-юридический кол |
| ЮЗАО «Фемида» Юридический колледж Российской академии правосудия |
| ЦАО «Связист» колледж связи №24 |
| ЮЗАО «Медики» Медицинский колледж №5 |
Пусть дискретная случайная величина  имеет закон распределения:
имеет закон распределения:

| 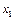
| 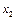
| … | 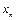
|
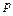
| 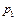
| 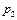
| 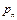
|
Характеристикой среднего значения случайной величины служит математическое ожидание.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие им вероятности:
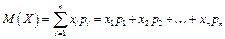 .
.
Свойства математического ожидания.
1. Математическое ожидание постоянной величины равно самой постоянной:
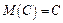 .
.
2. Постоянный множитель можно выносить за знак математического ожидания:
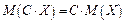 .
.
3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
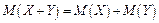 .
.
4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
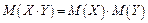 .
.
5. Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании:
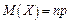 .
.
Рассеяние случайной величины около математического ожидания характеризуют дисперсия и среднее квадратическое отклонение.
Случайная величина 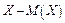 называется отклонением случайной величины от ее математического ожидания.
называется отклонением случайной величины от ее математического ожидания.
Замечание. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
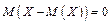 .
.
Случайная величина 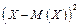 называется квадратом отклонения случайной величины от ее математического ожидания.
называется квадратом отклонения случайной величины от ее математического ожидания.
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
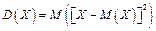 .
.
Для дискретной случайной величины дисперсию удобно вычислять по формуле:
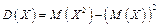 ,
,
где 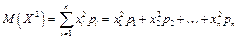 .
.
Свойства дисперсии.
1. Дисперсия постоянной величины равна нулю:
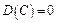 .
.
2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:
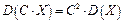 .
.
3. Дисперсия суммы двух независимых случайных величин равно сумме их дисперсий:
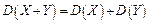 .
.
4. Дисперсия биномиального распределения равно произведению числа испытаний на вероятность появления и вероятность непоявления события в одном испытании:
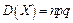 , где
, где 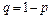 .
.
Средним квадратическим отклонением называется корень квадратный из дисперсии:
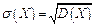 .
.
Задача 1. Дискретные случайные величины  ,
,  заданы законами распределения
заданы законами распределения 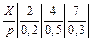 ,
, 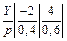 . Найти их числовые характеристики.
. Найти их числовые характеристики.
Решение.
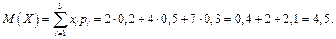
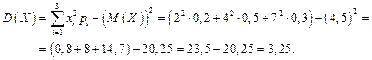
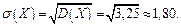
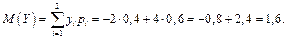
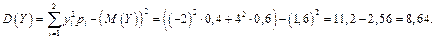
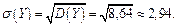
Ответ: 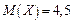 ,
, 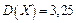 ,
, 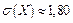 ;
;
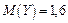 ,
, 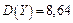 ,
, 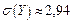 .
.
Задача 2. Независимые случайные величины  ,
,  имеют следующие числовые характеристики
имеют следующие числовые характеристики 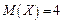 ,
, 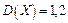 ,
, 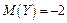 ,
, 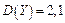 . Найти математическое ожидание и дисперсию случайных величин: а)
. Найти математическое ожидание и дисперсию случайных величин: а) 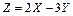 , б)
, б) 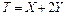 , в)
, в) 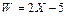 , г)
, г) 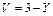 .
.
Решение.
а) 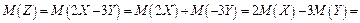
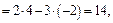
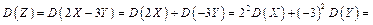
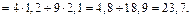
б) 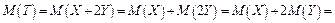
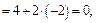
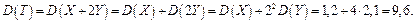
в) 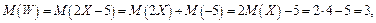
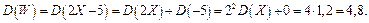
г) 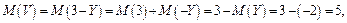
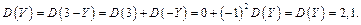
Ответ: 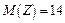 ,
, 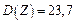 ;
; 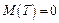 ,
, 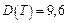 ;
;
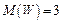 ,
, 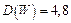 ;
; 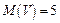 ,
, 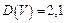 .
.
 2014-02-09
2014-02-09 376
376







