Функцией распределения случайной величины  называется функция
называется функция 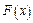 , определяющая для каждого значения
, определяющая для каждого значения 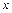 вероятность того, что случайная величина
вероятность того, что случайная величина  примет значение, меньшее
примет значение, меньшее 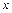 , т.е.
, т.е.
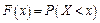 .
.
Часто вместо термина «функция распределения» используют термин «интегральная функция распределения».
Если функция распределения непрерывна на всей числовой прямой, то случайная величина называется непрерывной.
Свойства функции распределения 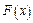 .
.
1. Значения функции распределения принадлежат отрезку 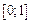 :
:
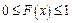 .
.
2. Функция распределения является неубывающей функцией:
если 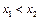 , то
, то 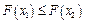 .
.
3. Вероятность того, что случайная величина  примет значение, заключенное в интервале
примет значение, заключенное в интервале 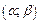 , равна приращению функции распределения на этом интервале:
, равна приращению функции распределения на этом интервале:
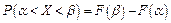 .
.
4. Вероятность того, что непрерывная случайная величина  примет одно определенное значение, например
примет одно определенное значение, например 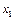 , равна нулю:
, равна нулю:
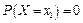 .
.
5. Если все возможные значения случайной величины  принадлежат интервалу
принадлежат интервалу 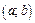 , то:
, то:
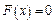 при
при 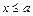 ;
; 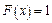 при
при 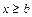 .
.
Задача 1. Дискретная случайная величина  задана законом распределения
задана законом распределения 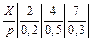 . Найти функцию распределения и построить ее график.
. Найти функцию распределения и построить ее график.
Решение. На числовую прямую нанесем возможные значения случайной величины  :
:

Они разбивают числовую прямую на четыре промежутка:
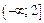 ,
, 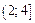 ,
, 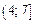 ,
, 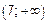 .
.
1) Пусть 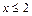 .
.

Значения, меньшие числа 2, случайная величина  принимать не может, поэтому
принимать не может, поэтому 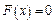 .
.
2) Пусть 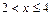 .
.
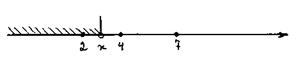
В заштрихованный промежуток попадает одно возможное значение случайной величины  , поэтому
, поэтому 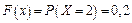 .
.
3) Пусть 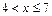 .
.
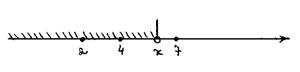
В заштрихованный промежуток попадают два возможных значения случайной величины  , поэтому
, поэтому
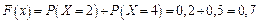 .
.
4) Пусть 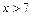 .
.
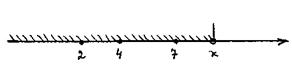
В заштрихованный промежуток попадают все возможные значения случайной величины  , поэтому
, поэтому 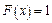 .
.
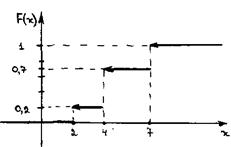
Итак, получили следующую функцию распределения:
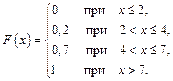
| 
|
Задача 2. Непрерывная случайная величина  задана функцией распределения
задана функцией распределения 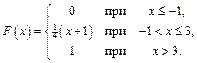 Найти вероятность того, что в результате испытания случайная величина
Найти вероятность того, что в результате испытания случайная величина  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 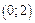 ,
, 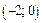 ,
, 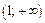 .
.
Решение. Применим формулу 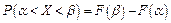 .
.
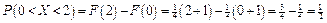 ;
;
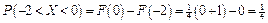 ;
;
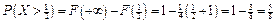 .
.
Ответ: 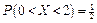 ,
, 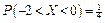 ,
, 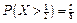 .
.
 2014-02-09
2014-02-09 408
408








