Плотностью вероятностей непрерывной случайной величины  называется функция
называется функция 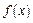 , равная производной функции распределения, т.е.
, равная производной функции распределения, т.е. 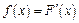 .
.
Часто вместо термина «плотность вероятностей» используют термин «дифференциальная функция распределения» или «плотность распределения».
Замечание. Зная плотность вероятностей, можно найти функцию распределения по формуле:
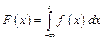 .
.
Свойства плотности вероятностей 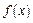 .
.
1. Плотность вероятностей неотрицательна, т.е. 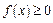 .
.
2. Вероятность того, что непрерывная случайная величина  примет значение, заключенное в интервале
примет значение, заключенное в интервале 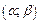 , определяется по формуле:
, определяется по формуле:
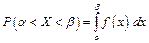 .
.
3. Несобственный интеграл от плотности вероятностей в пределах от 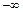 до
до 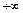 равен единице:
равен единице:
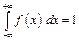 .
.
В частности, если все возможные значения непрерывной случайной величины принадлежат интервалу 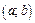 , то
, то 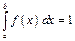 .
.
Задача 1. Непрерывная случайная величина  задана плотностью вероятностей
задана плотностью вероятностей 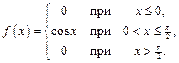
Найти функцию распределения.
Решение. Применим формулу 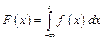 .
.
1) Пусть 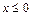 .
.
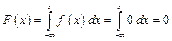 .
.
2) Пусть 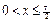 .
.
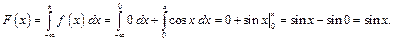
3) Пусть 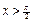 .
.
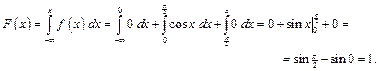
Итак, получили 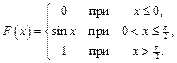
Задача 2. Непрерывная случайная величина  задана функцией распределения
задана функцией распределения 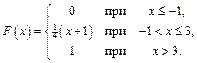
Найти плотность вероятностей.
Решение. Применим формулу 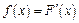 .
.
1) Пусть 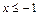 .
. 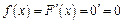 .
.
2) Пусть 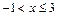 .
. 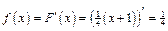 .
.
3) Пусть 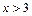 .
. 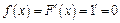 .
.
Итак, получили 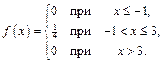
 2014-02-09
2014-02-09 274
274







