2014-02-09
1077
Рассмотрим плоскую манипуляционную систему с тремя степенями подвижности – двумя поступательными (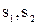
) и одной вращательной (θ). Одна нелинейность и одна избыточная степень подвижности составляют тот минимальный уровень, при котором проявляются важные специфические особенности манипуляционной системы и вместе с тем сохраняются простота движений манипуляционной системы с избыточностью. Функция положения элементарной манипуляционной системы имеет следующий вид:
|
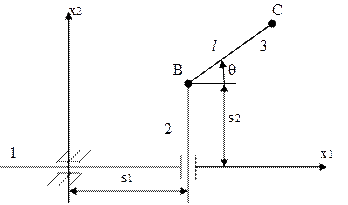| Элементарная манипуляционная система |
Для аналитического описания границы Γ рабочего пространства плоской манипуляционной системы используем следующее необходимое условие: в любой точке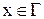 
этой границы допустимые перемещения 
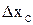захвата манипуляционной системы должны лежать в полуплоскости, ограниченной касательной к Γ в точке x. Другими словами, скалярное произведение 
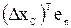, где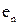 
– единичный вектор нормали к Γ в точке x, должно быть знакопостоянным.
Применительно к элементарной манипуляционной системе имеем:
|
|
|
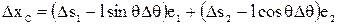
где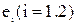 
- единичные векторы координатных осей 
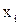. Отсюда
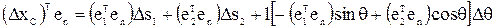(3)
Для знакопостоянства правой части (3) все входящие в нее слагаемые должны иметь одинаковый знак при изменении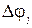 
. Значит, для каждого слагаемого должно выполняться одно из следующих условий: 1) значение 
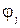является предельным и знак 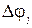постоянен; 2) коэффициент при 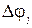обращается в нуль. Участки границы Γ можно классифицировать в зависимости от того, какое из указанных условий выполняется для каждой из обобщенных координат.
Пусть ограничения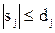 
наложены только на перемещения 
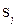поступательных пар элементарной манипуляционной системы, а угол поворота θ неограничен.
Выделим участки границы Γ трех типов: 1) параллельные оси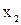 
, где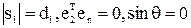 
, т.е. отлично от нуля лишь первое слагаемое в (3); 2) параллельные оси 
, где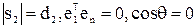 
; 3) дуги окружностей, где 
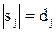. Очевидно, сформулированным необходимым условиям удовлетворяют по четыре варианта значений 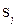, θ для случаев 1) и 2) и в общей сложности восемь дуг окружностей с центральным углом π/2 каждая и центрами 
.
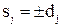На рисунке показаны границы рабочего пространства элементарной манипуляционной системы при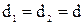 
, когда 
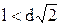(а) и 
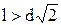(б).
| 
|
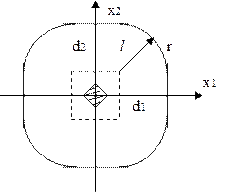| а) | б) |
| Рабочая зона элементарной манипуляционной системы |
Достаточные условия, выделяющие границу рабочего пространства манипуляционной системы, неизбежно должны быть нелокальными, т.е. должны учитывать все возможные решения задачи позиционирования в точке x. Сложность отыскания всех таких решений приводит к тому, что при построении границ рабочего пространства аналитические методы следует дополнять геометрическими.
В частности, для элементарной манипуляционной системы геометрический анализ позволяет найти уравнения границ рабочего пространства, а также оценку V свойства достижимости:
|
|
|
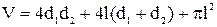
при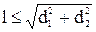 
; в противном случае из V следует вычесть площадь области, заштрихованной на рисунке б). Наконец, значения 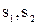для решений задачи позиционирования в точке x строятся как координаты точек окружности радиуса l с центром в x, лежащих в прямоугольнике 
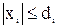; в силу двигательной избыточности элементарной манипуляционной системы задача позиционирования допускает непрерывное множество решений.
Метод ε-сети
Метод ε-сети позволяет получить приближенное решение задачи нахождения рабочей зоны манипулятора. Под ε-сетью в рабочем пространстве манипуляционной системы будем понимать конечную совокупность {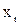
} его точек, обладающую тем свойством, что для любой точки 
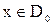найдется достаточно близкая к ней точка 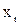, т.е.
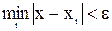. (4)
Идея излагаемого подхода заключается в том, чтобы, построив предварительную ε-сеть {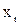}, использовать условие (4) как критерий принадлежности точки x рабочему пространству. Если (4) нарушается, то, согласно определению ε-сети, x лежит вне 
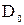. Однако, если (4) выполнено, то либо 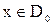, либо достаточно близко к границе .
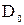Область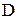 
- геометрическое место точек, удовлетворяющих (4), будет рассматриваться как некоторая аппроксимация неизвестной области 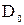, а ее объем V=V(D) будет служить оценкой искомой величины V(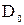) объема рабочего пространства. Чтобы вычислить V(D), применим (4) ко всем узлам кубической решетки с шагом δ. Тогда, очевидно,
,
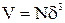где N – число таких узлов, удовлетворяющих условию (4).
Для построения ε-сети необходимо сформировать последовательности обобщенных координат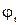 
, вычислить соответствующие точки 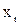и на основе критерия (4) построить ε-сеть. Существует несколько разных способов решения этой задачи: метод n-мерной кубической решетки, метод ЛП-последовательностей и др. Все они имеют свои плюсы и недостатки. Описание этих методов можно найти в специфической литературе.
