В структурном отношении геометрия манипуляционной системы сравнительно проста. Как уже было сказано, манипуляционная система представляет собой цепочку звеньев, последовательно соединенных кинематическими парами. Однако пространственное расположение звеньев и изменения конфигурации системы в процессе ее движения вносят определенные трудности в задачи описания ее геометрических, кинематических и динамических характеристик.
Для такого описания используют разные методы: аналитические, геометрические, векторные. Нами используется главным образом матричный метод, обладающий рядом преимуществ: простотой и наглядностью записи формул; удобством применения для численных расчетов; единообразием использования для анализа как разомкнутых, так и замкнутых кинематических цепей. Иначе эту задачу можно описать как прямую задачу кинематики (ПЗК), решение которой можно найти во множестве источников. Ниже представлен один из возможных вариантов решения.
Наглядность применения матричного метода обусловлена возможностью геометрической интерпретации матрицы как преобразования векторов, описывающих одну и ту же точку пространства в различных системах координат. Основная идея его заключается в следующем. С каждым звеном манипуляционной системы связывается определенная система координат, при этом к стойке отнесена неподвижная, базовая система. Переход от j-й системы координат, отвечающей j-му звену, к предыдущей (j-1)-й системе описывается линейным преобразованием, параметры которого зависят лишь от значений обобщенных координат связывающей эти звенья j-й кинематической пары. Если определить для каждой кинематической пары манипуляционной системы соответствующее преобразование, то координаты всех точек любого из звеньев в базовой системе координат находятся путем последовательного выполнения таких преобразований.
Координатные оси 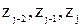 совместим с осями кинематических пар с номерами j-1, j, j+1, а их направления выберем произвольно. Координатные оси
совместим с осями кинематических пар с номерами j-1, j, j+1, а их направления выберем произвольно. Координатные оси 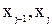 совпадают с прямыми, являющимися общими перпендикулярами к осям
совпадают с прямыми, являющимися общими перпендикулярами к осям 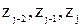 соответственно. Общий перпендикуляр определяется однозначно, если пара прямых непараллельна; в случае параллельных осей, например
соответственно. Общий перпендикуляр определяется однозначно, если пара прямых непараллельна; в случае параллельных осей, например 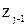 и
и 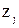 выберем положение общего перпендикуляра
выберем положение общего перпендикуляра 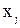 так, чтобы он проходил через точку
так, чтобы он проходил через точку 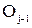 . Ось
. Ось 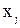 направлена от
направлена от 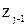 к
к 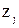 . Наконец, ось
. Наконец, ось 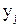 выберем так, чтобы получить правую систему координат. Построенные координатные системы непосредственно связаны с соответствующими звеньями кинематической цепи, так как положение осей кинематических пар, соединяющих каждое звено с предыдущим и последующим, фиксировано по отношению к этому звену. Если обозначить
выберем так, чтобы получить правую систему координат. Построенные координатные системы непосредственно связаны с соответствующими звеньями кинематической цепи, так как положение осей кинематических пар, соединяющих каждое звено с предыдущим и последующим, фиксировано по отношению к этому звену. Если обозначить 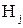 точку пересечения осей
точку пересечения осей 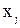 и
и 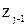 , то взаимное расположение j-й и (j-1)-й координатных систем описывается следующими параметрами:
, то взаимное расположение j-й и (j-1)-й координатных систем описывается следующими параметрами: 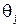 - угол между осью
- угол между осью 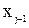 и лучом, проведенном через точку
и лучом, проведенном через точку 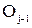 параллельно оси
параллельно оси 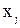 ;
; 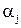 - угол между осями
- угол между осями 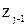 и
и 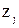 ;
; 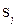 - алгебраическая длина отрезка
- алгебраическая длина отрезка 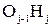 ;
; 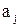 - алгебраическая длина отрезка
- алгебраическая длина отрезка 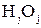 (
(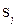 и
и 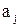 могут принимать как положительные так и отрицательные значения – в зависимости от порядка расположения концов отрезков на соответствующих осях). Другими словами, чтобы получить j-ю систему координат из (j-1)-й, нужно выполнить следующие преобразования: повернуть последнюю на угол
могут принимать как положительные так и отрицательные значения – в зависимости от порядка расположения концов отрезков на соответствующих осях). Другими словами, чтобы получить j-ю систему координат из (j-1)-й, нужно выполнить следующие преобразования: повернуть последнюю на угол 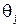 вокруг оси
вокруг оси 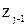 , чтобы обеспечить параллельность
, чтобы обеспечить параллельность 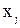 и
и 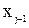 ; сдвинуть начало координат на величину
; сдвинуть начало координат на величину 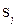 вдоль оси
вдоль оси 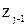 и на величину
и на величину 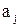 вдоль нового направления оси
вдоль нового направления оси 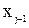 (т.е. по оси
(т.е. по оси 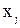 ), чтобы совместить его с точкой
), чтобы совместить его с точкой 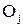 ; повернуть на угол
; повернуть на угол 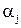 вокруг оси
вокруг оси 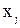 , чтобы совместить оси
, чтобы совместить оси 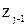 и
и 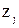 . Если записать эти преобразования в матричной форме, то поворотам отвечает умножение векторов на матрицы
. Если записать эти преобразования в матричной форме, то поворотам отвечает умножение векторов на матрицы
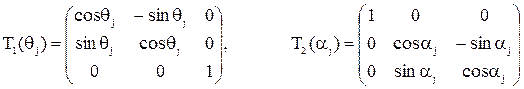 ,
,
а сдвигам – прибавление векторов

В результате векторы 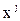 и
и 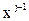 в j-й и (j-1)-й системах координат связаны так:
в j-й и (j-1)-й системах координат связаны так:
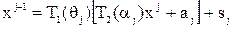 .
.
Для более компактной записи таких преобразований используются матрицы размерности 4x4. Матрицы 4x4 определяют одновременно и поворот и сдвиг системы координат:
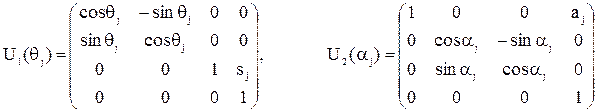 .
.
Благодаря этому векторы 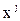 и
и 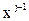 в j-й и (j-1)-й системах координат связаны так:
в j-й и (j-1)-й системах координат связаны так:
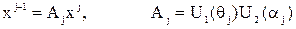 .
.
Более подробно с этим методом можно ознакомиться в литературе.
 2014-02-09
2014-02-09 1534
1534
