Пример 2. Пусть дан граф типа дерева - на рис

Пусть дан граф типа дерева - 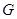на рис. 4.5 Сколько вершин максимального типа имеется в данном графе? Каково цикломатическое число графа? Чему равно цикломатическое число графа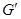, являющегося лесом и представленного двумя одинаковыми деревьями 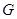? Построить ориентированное дерево с корнем 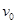, являющимся вершиной максимального типа.

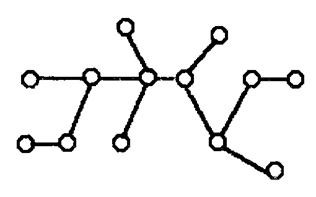
Рис. 4.5. Граф G типа дерево

Типы вершин графа отмечены на рис. 4.6,а, граф содержит две вершины максимального (4 - го) типа.

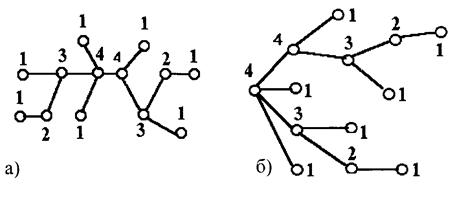
Рис. 4.6. Граф G типа дерево а) типы вершин, б) ориентированное дерево с корнем .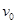

Цикломатическое число любого дерева 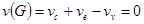. Действительно, число вершин 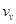в дереве на единицу больше числа ребер 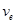(см. выше), т.е. 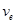-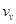= = -1, а число связных компонент графа типа дерева 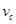= 1. Таким образом, цикломатическое число любого дерева, в том числе графа 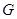, v = 0.

Цикломатическое число леса равно сумме цикломатических чисел своих связных компонент – деревьев, т.е. также равно нулю; таким образом, 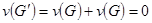, где 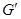- граф, представленный двумя одинаковыми деревьями G.

Построенное из н–графа G ориентированное дерево с корнем, являющимся вершиной максимального типа 4 (левая вершина – на рис. 3,а, изображено на рис. 3,б.