Дерево и лес

Н–граф называется неориентированным деревом (или просто деревом), если он связен и не содержит циклов, а значит петель и кратных ребер.

Дерево – минимальный связный граф в том смысле, что при удалении хотя бы одного ребра он теряет связность не содержащий циклов. Наличие этих двух свойств (связности и отсутствия циклов) позволяет жестко связать число вершин и число ребер: в дереве с n вершинами всегда n-1 ребро.

Лес - несвязный н–граф без циклов; связные компоненты леса являются деревьями. Любая часть леса или дерева также не имеет циклов, т.е. является лесом или деревом. Любая цепь в таком графе – простая, иначе она содержала бы цикл.

В неориентированном дереве между любыми двумя вершинами существует цепь и притом только одна. Верно и обратное: если любые две вершины графа связаны единственной цепью, то граф является деревом.

Вершина v графа G называется концевой или висячей если ее степень 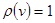. Ребро, инцидентное концевой вершине называется концевым. Если конечное дерево состоит более чем из одной вершины, оно имеет хотя бы две концевые вершины и хотя бы одно концевое ребро.

Ориентация неориентированного дерева осуществляется следующим образом. В дереве G отмечается(выбирается) вершина 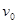- так называемый корень дерева G, и все ребра такого дерева с корнем ориентируются от этой вершины – корня. Вершину 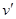ребра 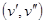можно соединить единственной цепью L с корнем 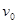. Если эта цепь не содержит ребра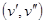, в это ребро вводится ориентация от 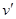к 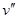, в противном случае – от 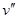к 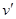. Такая ориентация согласована с ориентацией того же ребра, определенной через вершину 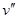.Данная ориентация дерева с корнем 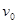единственна. Ориентированное таким образом дерево с корнем называется ориентированным деревом. В нем все ребра имеют направление от корня. При выборе другой вершины – корня получаем другой орграф – дерево.

Пусть v - вершина дерева G с корнем 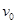;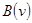- множество всех вершин, связанных с корнем цепями, проходящими через вершину v. Это множество порождает подграф 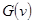, называемый ветвью вершины v в дереве с корнем 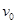. Если дерево имеет более двух вершин, то среди них есть некоторые вершины.

Пусть дано конечное дерево G. Вершинами типа 1 называют его концевые вершины. Если из дерева G удалить все вершины типа 1 и инцидентные им концевые ребра, то в оставшемся дереве 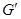концевые вершины называют вершинами типа 2 в дереве G. Аналогично определяются вершины типов 3, 4 и т.д. Конечное дерево имеет вершины лишь конечного числа типов, причем число вершин максимального типа равно единице или двум.

Цикломатическим числом конечного н–графа G называется 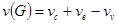, где 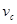- число связных компонент графа; 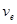- число его ребер; 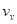- число вершин. Цикломатическое число любого конечного н–графа неотрицательно.