Пример. Рассмотрим один блок изображения

Рассмотрим один блок изображения

После удаления среднего значения 128 из каждого элемента X и выполнения ДКП матрица Y имеет вид:

Пока никакого сжатия не произошло. Отметим, что по сравнению с X вматрице Y коэффициенты с большими амплитудами сосредоточены около коэффициента y₀₀, называемого коэффициентом постоянного тока. Такая ситуация типична и именно это явление используется для сжатия изображений. Процесс квантования, который ведет к сжатию коэффициентов ДКП, выражается следующим образом

z_kl = round(y_kl /q_kl) = [(y_kl ±[q_kl /2]) /q_kl], k,l = 0,1,...,7,

где q_kl обозначает kl -й элемент матрицы квантования Q размера 8x8 ([x] обозначает наибольшее целое, меньшее или равное x). Для нашего примера выберем матрицу Q вида

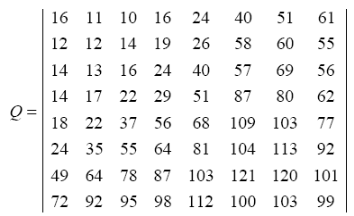
Тогда квантованный выход ДКП имеет вид

В результате квантования произошло обнуление многих коэффициентов y_kl. Выбор матрицы Q определяется требуемым коэффициентом сжатия. Очевидно, что процесс квантования существенно экономит биты, необходимые для представления исходного изображения, т.к. только 11 ненулевых значений необходимы для представления Z вместо исходных 64 значений, необходимых для представления X. Таким образом, можно говорить о том, что уже получено сжатие с коэффициентом К=64/11≈5.8. Матрица Z может быть эффективно представлена с использованием кодирования длин серий и кодирования кодом Хаффмана.

Декодирование начинается с восстановления из полученного битового потока закодированных неравномерным кодом длин серий нулей и значащих элементов матрицы Z. Так как кодирование коэффициентов матрицы Z выполняется без потерь, то декодер восстанавливает точное значение Z.

Восстановление оценок коэффициентов разложения 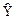по квантованным значениям Z выполняется по формуле

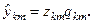
В рассматриваемом примере получим

Теперь декодер выполняет обратное 8х8 ДКП для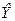. Выход преобразователя имеет вид:

Очевидно, что 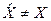и причина этого несовпадения (ошибки кодирования) лежит в квантовании коэффициентов ДКП.