Формулы математической логики.
Формулой математической логики называется сложное высказывание, которое получено из элементарных высказываний с использованием логических операций.
Две формулы равносильны, если они принимают одинаковые логические значения на любом наборе значений входящих в формулу элементарных высказываний. Равносильность формул обозначается - A º B.
1) Коммутативность
АVВ º ВVА А&В º В&А
2) Ассоциативность
АV(ВVС) º (АVВ)VС А&(В&С) º (А&В) &С
3) Дистрибутивность
АV(В&С) º (АVВ)&(АVС) А&(ВVС) º (А&В)V(А&С)
4) Идемпотентность
АVА º А А&А º А
5) Поглощение
АV(А&В) º А А&(АVВ) º А
6) Закон де Моргана
 º
º 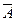 &
&
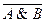 º
º 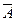 V
V
7) Закон исключающий третьего
АV1 º 1 А&1 º A
8) Закон противоречия
AVÆ º A A&Æ º Æ
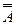 º A
º A
10)  º 1,
º 1,  º 0
º 0
11) A®B º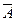 VB
VB
12) A«B º (A®B)&(B®A)
13) AÅB º A& V
V 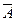 &B
&B
14) A | B º 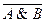 º
º 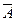 V
V
15) A¯B º 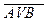 º
º 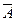 &
&
ПРИМЕР
Доказать: 
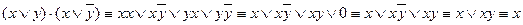
Представление произвольной функции алгебры логики в виде формулы алгебры логики
Пусть 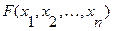 - произвольная функция алгебры логики
- произвольная функция алгебры логики  переменных.
переменных.
Рассмотрим формулу
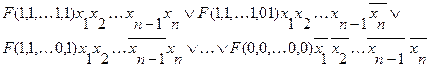 (2.1)
(2.1)
которая составлена следующим образом: каждое слагаемое этой логической суммы представляет собой конъюнкцию, в которой первый член является значением функции  при некоторых определенных значениях переменных
при некоторых определенных значениях переменных  , остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0..
, остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0..
Вместе с тем формула (2.1) содержит в виде логических слагаемых всевозможные конъюнкции указанного вида.
Ясно, что формула (2.1)полностью определяет функцию  . Иначе говоря, значения функции
. Иначе говоря, значения функции  и формулы (2.1) совпадают на всех наборах значений переменных
и формулы (2.1) совпадают на всех наборах значений переменных  . То есть функция
. То есть функция
Составление формул по таблице истинности.  может быть представлена в виде:
может быть представлена в виде:
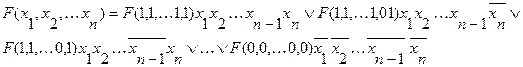 (2.2)
(2.2)
ПРИМЕР Пусть функция  имеет следующую таблицу истинности:
имеет следующую таблицу истинности:
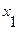 | 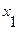 | 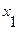 | 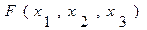 |
Тогда функция  может быть определена в следующем виде:
может быть определена в следующем виде:


Нетрудно заметить, что для определении функции берутся только те наборы переменных  , при которых функция принимает значения 1, что значительно упрощает процедуру определения функции
, при которых функция принимает значения 1, что значительно упрощает процедуру определения функции  .
.
Формула (2.1) обладает свойствами:
1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию 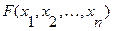 .
.
2. Все логические слагаемые формулы различны.
3. Ни одно логическое слагаемое формулы не содержит одновременно переменную и ее отрицание.
4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
5. Перечисленные свойства называются свойствами совершенства.
 2014-02-09
2014-02-09 1049
1049








