Как и любая точная наука, алгебра логики опирается на некоторые аксиомы и законы, позволяющие доказывать равносильность формул, упрощать формулы и приводить их к заданному виду, не прибегая к построению таблиц истинности. Это практически всегда дает более короткий и менее громоздкий путь, чем построение таблиц истинности.
Рассмотрим эти аксиомы и законы, объединив их в несколько групп.
I. Аксиомы одиночных элементов:
1) 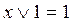 ; 2)
; 2) 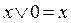 ;
;
3) 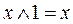 ; 4)
; 4) 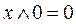 .
.
II. Аксиомы и законы отрицания:
1) 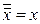 ; 2)
; 2) 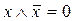 (закон противоречия); 3)
(закон противоречия); 3) 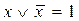 (закон исключенного третьего);
(закон исключенного третьего);
4) 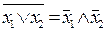 ; 5)
; 5) 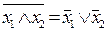 (законы де Моргана).
(законы де Моргана).
|
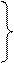 1)
1) 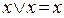 (общий случай
(общий случай 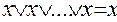 );
); 
2) 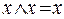 (общий случай
(общий случай 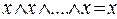 );
);
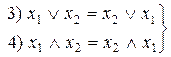 – переместительные законы;
– переместительные законы;
|
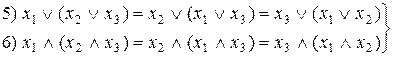 – сочетательные
– сочетательные Сочетательные законы говорят о том, что если формула состоит из нескольких высказываний, соединенных операцией дизъюнкции или конъюнкции, то очередность выполнения операций над высказываниями может быть любая, или, другими словами, в такой формуле можно опускать скобки:
7) 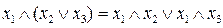 – распределительный (дистрибутивный) закон первого рода;
– распределительный (дистрибутивный) закон первого рода;
8) 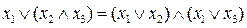 – распределительный (дистрибутивный) закон второго рода.
– распределительный (дистрибутивный) закон второго рода.
Из распределительного закона первого рода непосредственно вытекает, что если формула состоит из двух и более конъюнкций, соединенных знаками дизъюнкции, и каждая конъюнкция имеет общий сомножитель, то его можно выносить за скобки.
Из второго распределительного закона следует, что если формула состоит из двух и более заключенных в скобки дизъюнкций, соединенных знаком конъюнкции, то скобки можно логически перемножать.
Действительно, возьмем правую часть закона 8 и выполним логическое перемножение скобок:
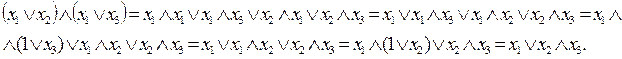
То есть мы получили левую часть закона 8, логически перемножив скобки.
IV. Некоторые важные равносильности:
1) 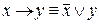 ; 2)
; 2) 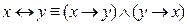 ;
;
3) 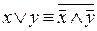 ; 4)
; 4) 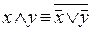 .
.
Равносильности 3 и 4 вытекают из законов де Моргана и аксиомы двойного отрицания.
V. Закон двойственности.
Пусть формула 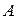 содержит только операции конъюнкции, дизъюнкции и отрицания. Операцию конъюнкции называют двойственной операции дизъюнкции, и наоборот.
содержит только операции конъюнкции, дизъюнкции и отрицания. Операцию конъюнкции называют двойственной операции дизъюнкции, и наоборот.
Определение. Формулы 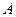 и
и 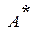 называются двойственными, если формула
называются двойственными, если формула 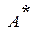 получена из формулы
получена из формулы 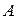 путем замены в ней каждой операции на двойственную. Например:
путем замены в ней каждой операции на двойственную. Например: 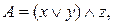
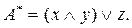
Свойства операций импликации и эквивалентности, вытекающие из приведенных выше равносильностей, следующие:
1. Операция импликации не обладает переместительным свойством (законом).
Действительно: 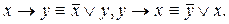
 Отсюда видим, что
Отсюда видим, что 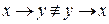 .
.
2. Операция импликации не обладает сочетательным свойством (законом).
Действительно: 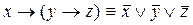 ;
; 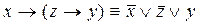 ;
; 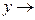
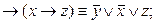
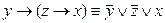 ;
; 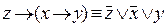 ;
;
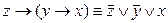 . Видим, что в общем случае для операции импликации не выполняется сочетательный закон, так как не все формулы, содержащие три (и более) высказывания, соединенных знаком
. Видим, что в общем случае для операции импликации не выполняется сочетательный закон, так как не все формулы, содержащие три (и более) высказывания, соединенных знаком 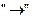 , но занимающих в формуле разные местоположения, оказываются равносильными. Другими словами, в формуле, содержащей несколько знаков
, но занимающих в формуле разные местоположения, оказываются равносильными. Другими словами, в формуле, содержащей несколько знаков 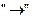 ,нельзя опускать скобки.
,нельзя опускать скобки.
3. Операция эквивалентности обладает переместительным свойством.
Действительно, на основании равносильностей IV.2 и IV.1, имеем:
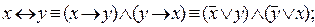
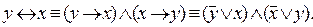
Правая часть последней равносильности есть конъюнкция. На основании переместительного свойства операции дизъюнкции имеем 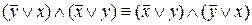 , что полностью совпадает с правой частью первой равносильности.
, что полностью совпадает с правой частью первой равносильности.
4. Операция эквивалентности обладает сочетательным свойством.
Действительно, построив таблицы истинности или выполнив соответствующие преобразования, можно показать, что выполняются равносильности 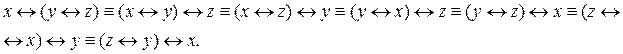
Подробные преобразования не приводим из-за их громоздкости.
Таким образом, для операции 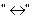 выполняется сочетательный закон и можно поэтому опускать скобки в формуле или какой-то ее части, где используются последовательно стоящие знаки
выполняется сочетательный закон и можно поэтому опускать скобки в формуле или какой-то ее части, где используются последовательно стоящие знаки 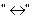 .
.
Используя аксиомы и законы алгебры логики, можно выполнять различные алгебраические преобразования и заменять одну формулу другой, ей равносильной. Это же самое можно делать и с помощью таблиц истинности, о чем говорилось в подразделе 1.3.
Однако последовательность выполнения операций при алгебраических преобразованиях имеет некоторые особенности. Мы их сейчас рассмотрим.
При построении таблиц истинности логические значения любой формулы получаются путем выполнения операций над цифрами 0 и 1. Поэтому операции могут выполняться как над одной цифрой (операция отрицания), так и над двумя (опять-таки операция отрицания и все остальные операции: 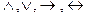 ).
).
Из этого следует, что при построении таблиц истинности последовательность выполнения операций определяется не только скобками (в скобках указываются, как минимум, два высказывания, соединенных знаками 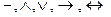 ), но и операцией отрицания, знак которой стоит над одним высказыванием.
), но и операцией отрицания, знак которой стоит над одним высказыванием.
При алгебраических преобразованиях операции выполняются не над цифрами 0 и 1, а над символами (буквами). Из этого следует, что операцию отрицания над одним высказыванием выполнить нельзя, так как результат будет неоднозначным – он будет зависеть от логических значений, принимаемых этим высказыванием. Любую другую операцию (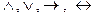 ) можно выполнять над двумя или большим числом высказываний. Поэтому в исходной формуле со скобками каждую пару скобок можно обозначить каким-либо символом. Пару новых символов, соединенных каким-либо знаком операции, можно опять обозначить новым символом. Продолжая этот процесс, мы дойдем до такого положения, когда у нас останутся только два символа, объединенных одним знаком операции. Преобразование исходной формулы, очевидно, можно начинать с этой последней операции и двигаться в направлении, обратном относительно порядка расстановки символов.
) можно выполнять над двумя или большим числом высказываний. Поэтому в исходной формуле со скобками каждую пару скобок можно обозначить каким-либо символом. Пару новых символов, соединенных каким-либо знаком операции, можно опять обозначить новым символом. Продолжая этот процесс, мы дойдем до такого положения, когда у нас останутся только два символа, объединенных одним знаком операции. Преобразование исходной формулы, очевидно, можно начинать с этой последней операции и двигаться в направлении, обратном относительно порядка расстановки символов.
Из сказанного выше следует, что алгебраические преобразования исходной формулы можно выполнять тремя способами:
1) от начала к концу, т.е. сначала выполнять наиболее приоритетные операции, двигаясь к менее приоритетным;
2) от конца к началу, т.е. двигаясь от менее приоритетных к более приоритетным операциям;
3) комбинируя предыдущие два способа.
Рассмотрим более детально прямой порядок выполнения алгебраических преобразований. Будем считать, что в исходной формуле скобки расставлены правильно, т.е. они расставлены так, что их расположение в формуле однозначно определяет порядок выполнения операций. Причем в скобки не заключаются одиночные высказывания, входящие в формулу с отрицанием или без него. То есть вместо записи 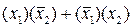 всегда пишут
всегда пишут 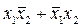 или вместо
или вместо 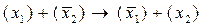 пишут
пишут 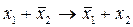 и т.д. Как уже говорилось, в скобки могут заключаться два и более высказывания, соединенных одним из знаков операций (
и т.д. Как уже говорилось, в скобки могут заключаться два и более высказывания, соединенных одним из знаков операций (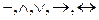 ). При этом одна пара скобок не может содержать больше одной операции, не обладающей переместительным и сочетательным свойством (операция
). При этом одна пара скобок не может содержать больше одной операции, не обладающей переместительным и сочетательным свойством (операция 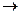 ). То есть запись
). То есть запись 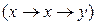 является некорректной, или, иначе, не является формулой. В такой записи предполагается безразличным порядок выполнения операций, т.е. операция
является некорректной, или, иначе, не является формулой. В такой записи предполагается безразличным порядок выполнения операций, т.е. операция 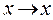 или
или 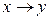 выполняется раньше. Но в данном случае от порядка выполнения операций зависит результат. Поэтому если формула записывается с использованием нескольких знаков
выполняется раньше. Но в данном случае от порядка выполнения операций зависит результат. Поэтому если формула записывается с использованием нескольких знаков 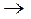 , то использование скобок обязательно.
, то использование скобок обязательно.
Предыдущая запись выражения будет формулой, если ввести скобки 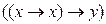 или
или 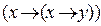 . При этом
. При этом
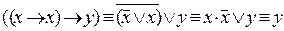 ;
; 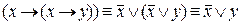 .
.
В то же время выражения 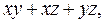
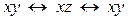 скобок не требуют, т.е. являются формулами, так как, учитывая приоритет операций, мы можем однозначно установить правильный порядок их выполнения.
скобок не требуют, т.е. являются формулами, так как, учитывая приоритет операций, мы можем однозначно установить правильный порядок их выполнения.
Самыми простыми являются выражения, состоящие из одиночных высказываний, входящих в эти выражения с отрицанием или без него и соединенных знаком 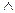 или
или 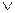 . Такие выражения упрощению уже не поддаются, но могут преобразовываться одно в другое. Считается, что такие выражения обладают равной сложностью.
. Такие выражения упрощению уже не поддаются, но могут преобразовываться одно в другое. Считается, что такие выражения обладают равной сложностью.
Выражения в скобках, в которых высказывания соединены некоторым знаком операции, можно упростить, применив к ним операции меньшей сложности.
Приведем пример упрощения формулы, используя прямой порядок выполнения операций: 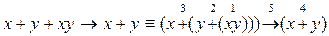 . Так как выражение в самых внутренних скобках упростить нельзя, операцию с номером 1 не выполняем, а переходим сразу к операции с номером 2.
. Так как выражение в самых внутренних скобках упростить нельзя, операцию с номером 1 не выполняем, а переходим сразу к операции с номером 2.
Используя правило поглощения 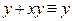 , получаем формулу
, получаем формулу 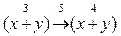 . Обе скобки уже упрощены до предела, поэтому, выполняя операцию с номером 5, будем иметь
. Обе скобки уже упрощены до предела, поэтому, выполняя операцию с номером 5, будем иметь 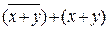 . Остается выполнить операцию отрицания. Выполнив её, используя закон де Моргана, получим формулу
. Остается выполнить операцию отрицания. Выполнив её, используя закон де Моргана, получим формулу 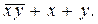
Так как для операции 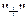 справедлив сочетательный закон, то во вторую пару скобок исходного выражения можно включить другие высказывания:
справедлив сочетательный закон, то во вторую пару скобок исходного выражения можно включить другие высказывания: 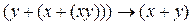 . Выполняя аналогичные преобразования, получим тот же результат.
. Выполняя аналогичные преобразования, получим тот же результат.
Приведем последовательное упрощение той же формулы, используя обратный порядок выполнения операций.
В формуле 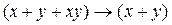 обозначим
обозначим 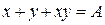 ,
, 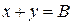 и будем выполнять операцию импликации над А и В:
и будем выполнять операцию импликации над А и В: 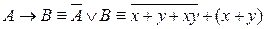 .
.
Снимем отрицание, применяя закон де Моргана, и получим формулу 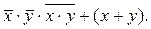 Снимая групповое отрицание
Снимая групповое отрицание 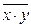 , получим формулу
, получим формулу 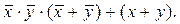 Применяя операцию конъюнкции к скобке, получим
Применяя операцию конъюнкции к скобке, получим 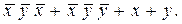 Используя аксиомы
Используя аксиомы 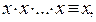 ,
, 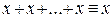 , получим формулу
, получим формулу 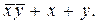
Как видим, получили тот же результат, что и при использовании прямого порядка выполнения операций.
Отметим еще одно чрезвычайно важное свойство функциональной полноты системы операций. Если любую формулу алгебры логики можно свести к некоторой другой равносильной формуле, содержащей только определенную систему операций, то такая система операций называется функционально полной системой операций (ФПСО) или базисной. В алгебре логики такой ФПСО являются системы операций: 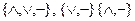 .
.
Покажем на примере, как логическая формула сводится к другой равносильной ей формуле, но содержащей только указанные системы операций. В предыдущих примерах было показано, что 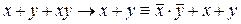 . То есть в левой формуле использовались операции
. То есть в левой формуле использовались операции 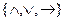 , а в правой – только операции
, а в правой – только операции 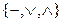 . Сведем правую формулу приведенной равносильности к формуле, содержащей только операции
. Сведем правую формулу приведенной равносильности к формуле, содержащей только операции 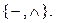
К формуле 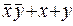 применим аксиому
применим аксиому 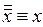 . Тогда можно записать:
. Тогда можно записать:
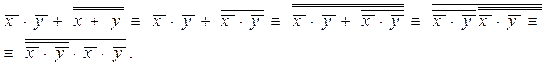
Ту же самую формулу сведем к равносильной ей формуле, содержащую только операции 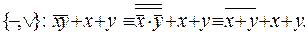
Таким образом, если говорят об упрощении формулы, то имеют в виду ее сведение к ФПСО.
3.4.1. Правила склеивания для элементарных конъюнкций и
дизъюнкций
Сначала введем некоторые понятия. Логическое произведение 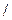 сумма любого числа высказываний называется элементарным, если сомножители
сумма любого числа высказываний называется элементарным, если сомножители 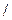 слагаемые в нем являются либо одиночными высказываниями, либо их отрицаниями.
слагаемые в нем являются либо одиночными высказываниями, либо их отрицаниями.
Например: 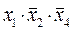 – элементарное произведение,
– элементарное произведение,
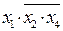 – неэлементарное произведение.
– неэлементарное произведение.
Количество сомножителей в элементарном произведении называется его рангом.
Два элементарных произведения одинакового ранга 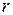 называются соседними, если они являются формулами одних и тех же высказываний и отличаются знаком отрицания только одного высказывания.
называются соседними, если они являются формулами одних и тех же высказываний и отличаются знаком отрицания только одного высказывания.
Теперь сформулируем само правило склеивания для элементарных конъюнкций: логическую сумму двух соседних произведений некоторого ранга 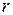 можно заменить одним элементарным произведением ранга
можно заменить одним элементарным произведением ранга 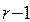 , являющимся общей частью исходных слагаемых.
, являющимся общей частью исходных слагаемых.
Пример: 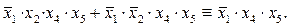
Аналогично для дизъюнкции определяются ранг и соседство. Правило склеивания для элементарных дизъюнкций формулируется следующим образом: логическое произведение двух соседних дизъюнкций ранга 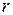 можно заменить одной дизъюнкцией ранга
можно заменить одной дизъюнкцией ранга 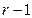 , являющейся общей частью исходных сомножителей.
, являющейся общей частью исходных сомножителей.
Пример: 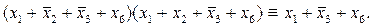
3.4.2. Правила поглощения для элементарных конъюнкций и
дизъюнкций
Логическую сумму двух элементарных конъюнкций разных рангов, из которых одна является частью другой, можно заменить слагаемым, имеющим меньший ранг.
Пример: 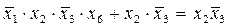 .
.
Правило поглощения для элементарных дизъюнкций формулируется следующим образом: логическое произведение двух элементарных дизъюнкций разных рангов, одна из которых является частью другой, можно заменить сомножителем меньшего ранга.
Пример: 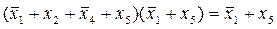 .
.
Правила склеивания и поглощения, как нетрудно заметить, являются следствием распределительных законов.
3.4.3. Правило развёртывания
Оно также является следствием распределительных законов и регламентирует действие, обратное склеиванию. Оно используется, когда нужно составить некоторое логическое выражение в виде совокупности конституент (от англ. constituent – составная часть чего-либо) единицы (КЕ) или конституент нуля (КН).
Конституента единицы (иногда употребляют минтерм)– это конъюнкция всех 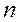 высказываний, которые входят в неё в прямом или инверсном виде лишь по одному разу и обращающаяся в ноль при одном наборе логических значений высказываний и в единицу при всех остальных наборах.
высказываний, которые входят в неё в прямом или инверсном виде лишь по одному разу и обращающаяся в ноль при одном наборе логических значений высказываний и в единицу при всех остальных наборах.
Конституента нуля (иногда употребляют макстерм) – это дизъюнкция всех 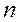 высказываний, которые входят в неё в прямом или инверсном виде лишь по одному разу и обращающаяся в единицу при одном наборе логических значений высказываний и в ноль при всех остальных наборах.
высказываний, которые входят в неё в прямом или инверсном виде лишь по одному разу и обращающаяся в единицу при одном наборе логических значений высказываний и в ноль при всех остальных наборах.
Количество KE и КН заданного числа высказываний 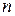 совпадает, как это следует из определения, с числом различных наборов высказываний и равно
совпадает, как это следует из определения, с числом различных наборов высказываний и равно 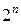 . Конституенты принято обозначать какими-либо символами, например:
. Конституенты принято обозначать какими-либо символами, например: 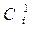 и
и 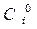 . Единица или ноль в верхнем индексе означает вид конституенты, т.е. КЕ это или КН, нижний индекс означает ее номер, совпадающий с номером набора.
. Единица или ноль в верхнем индексе означает вид конституенты, т.е. КЕ это или КН, нижний индекс означает ее номер, совпадающий с номером набора.
Приведем примеры всех КЕ и КН для двух высказываний.
Таблица 7
 2015-03-22
2015-03-22 5950
5950








