2014-02-09
1730
Пусть функция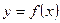 
определена в некоторой окрестности точки 
.
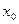Определение 15.4. Если существует предел отношения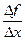 
при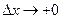 
(то есть 
, 
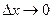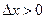), то этот предел называется правой производной функции 
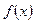в точке 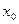и обозначается символом 
:
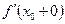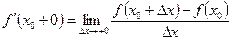. (15.6)
Определение 15.5. Если существует предел отношения 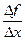при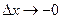 
(то есть , 
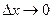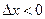), то этот предел называется левой производной функции 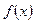в точке 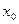и обозначается символом 
:
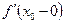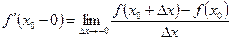. (15.7)
☼ Замечание 15.2. Для того чтобы существовала производная в точке 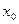, необходимо и достаточно, чтобы существовали левая и правая производные в этой точке и они были бы равны.☼
