Скорость движения. Кинематические характеристики криволинейного движения

Кинематические характеристики криволинейного движения

Производная вектора

Пусть вектор меняется по известному закону со временем.

.

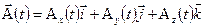Производная такого вектора по аргументу t вычисляется как производная сложной функции

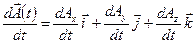
где: 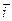,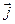и 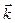— единичные векторы направлений x, y, z.

Зададим криволинейное движение частицы М зависимостью её радиус-вектора от времени (рис. 2.7):

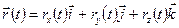. (2.7)

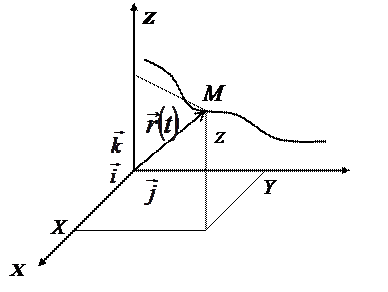
Рис. 2.7

Пусть 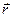и 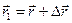— радиус-векторы частицы в моменты времени t и (t + D t) (рис. 2.8). Разность этих векторов 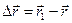называется вектором перемещения частицы.

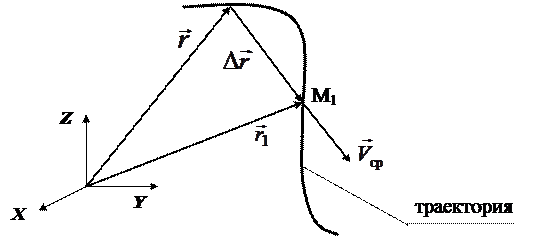
Рис. 2.8

По определению, вектором средней скорости движения в интервале времени от t до t + D t называется отношение вектора перемещения ко времени, за которое оно произошло:

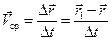. (2.8)

Направление вектора средней скорости совпадает с направлением вектора перемещения .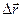

Если уменьшать интервал времени, устремляя его к нулю, то вектор средней скорости стремится к значению, которое называется мгновенная скорость:

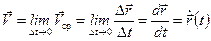(2.9)

Учитывая (2.7) запишем вектор мгновенной скорости в виде векторной суммы её составляющих по координатам x, y, z:

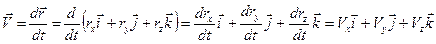(2.10)

где: V_x, V_y, V_z — проекции вектора скорости на оси x, y, z (рис. 2.9)

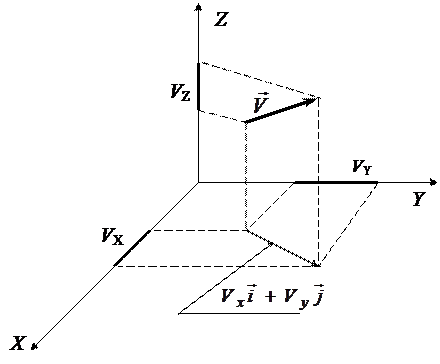
Рис. 2.9

Модуль вектора скорости

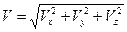
Вектор мгновенной скорости всегда направлен по касательной к траектории (рис. 2.10)

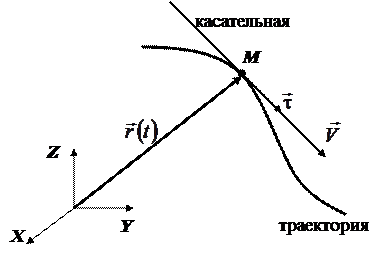
Рис. 2.10