Любое движение твёрдого тела может быть представлено суперпозицией двух движений — поступательного и вращательного.
Представим плоское движение тела суммой поступательного со скоростью 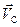 , равной скорости центра масс, и вращения с угловой скоростью
, равной скорости центра масс, и вращения с угловой скоростью 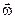 вокруг оси, проведённой через центр масс тела — точку С.
вокруг оси, проведённой через центр масс тела — точку С.
Скорость i -той частицы тела (D mi) будет равна векторной сумме её скоростей в этих двух движениях:
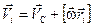 .
.
Здесь 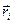 — радиус-вектор частицы, определяющий её положение относительно точки центра масс — С (рис. 10.4).
— радиус-вектор частицы, определяющий её положение относительно точки центра масс — С (рис. 10.4).
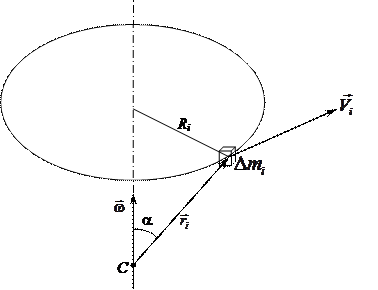
Рис. 10.4
Вычислим кинетическую энергию i -той частицы:
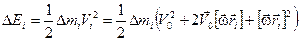 .
.
Заметим (см. рис. 10.4), что модуль векторного произведения 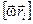 равен:
равен:
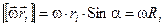 ,
,
где Ri — радиус круговой траектории частицы D mi, или, что то же самое, — её расстояние от оси вращения.
Теперь раскроем скобки, попутно сделав циклическую перестановку сомножителей во втором слагаемом:
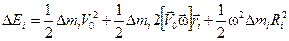 .
.
Кинетическая энергия тела равна сумме энергий всех её частиц, поэтому:
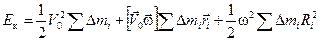 .
.
Анализируя этот результат, приходим к следующим выводам:
Сумма 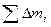 = М равна массе тела.
= М равна массе тела.
Сумма 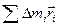 равна произведению массы тела на радиус-вектор точки центра масс
равна произведению массы тела на радиус-вектор точки центра масс 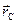 . Но так как в этой задаче все радиус-векторы откладываются от точки центра масс, то
. Но так как в этой задаче все радиус-векторы откладываются от точки центра масс, то 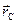 = 0, и
= 0, и 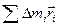 =
= 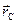 = 0.
= 0.
Сумма 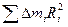 = I C представляет собой момент инерции тела относительно оси вращения, проходящей через центр масс (точку С).
= I C представляет собой момент инерции тела относительно оси вращения, проходящей через центр масс (точку С).
Таким образом, кинетическая энергия тела равна:
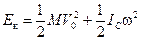 . (10.8)
. (10.8)
Представив движение суммой поступательного и вращательного движений, мы пришли к выводу, что кинетическая энергия плоского движения равна сумме энергий поступательного движения со скоростью, равной скорости центра масс VС и вращения относительно оси, проходящей через центр масс тела:
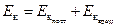 .
.
 2014-02-09
2014-02-09 1396
1396








