По существу валентные электроны перенормируют потенциал ионного остова благодаря кулоновской экранировке и парному корреляционному взаимодействию. Тем не менее, благодаря периодичности кристалла можно ввести эффективный одноэлектронный потенциал 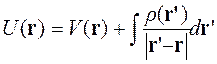 , обладающий свойствами периодичности кристалла.
, обладающий свойствами периодичности кристалла.
Поэтому рассмотрим одноэлектронное приближение с периодическим потенциалом для которого уравнение Шредингера имеет вид
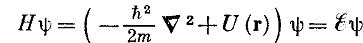 .
.
Теорема Блоха: Собственные состояния гамильтониана H с периодическим потенциалом
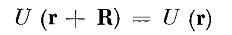
для всех векторов решетки Браве R, могут быть выбраны так, чтобы их волновые функции имели вид плоской волны, умноженной на функцию с периодичностью решетки Браве, т.е.
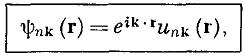
где
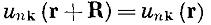 .
.
В связи с этим электроны в кристалле называют блоховскими электронами (в отличие от свободных электронов).
Из этой теоремы следует также равенство
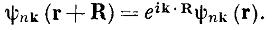 (**)
(**)
И наоборот, из последнего соотношения для всех векторов решетки Браве R следует первое определение. Поэтому вторая формулировка теоремы Блоха – собственные значения состояния 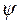 оператора
оператора 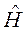 можно выбрать таким образом, чтобы с каждым из них был связан некоторый вектор
можно выбрать таким образом, чтобы с каждым из них был связан некоторый вектор 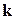 такой, что для любого вектора прямой решетки Браве
такой, что для любого вектора прямой решетки Браве 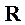 выполнялось равенство (**)
выполнялось равенство (**)
Доказательство теоремы Блоха для невырожденных состояний.
Свойство трансляционной инвариантности гимильтониана для любых векторов решетки Браве
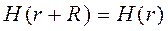 .
.
Рассмотрим два эквивалентных уравнения Шредингера
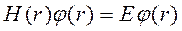 и
и 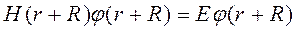 .
.
С учетом трансляционной инвариантности для векторов решетки Браве R=m a 1+n a 2+p a 3 имеем
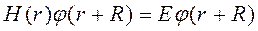 .
.
Следовательно, имеется семейство вырожденных собственных решений, отличающихся сдвигом на период решетки Браве. Так как мы предположили отсутствие вырождения состояний, то эти решения отличаются только постоянным множителем, т.е. 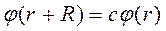 . Так, при сдвиге на один шаг решетки будем иметь
. Так, при сдвиге на один шаг решетки будем иметь 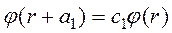 , где в силу нормировки волновой функции
, где в силу нормировки волновой функции 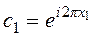 , где x1 – некоторое число, характеризующее изменение фазы решения Шредингера при элементарном сдвиге.
, где x1 – некоторое число, характеризующее изменение фазы решения Шредингера при элементарном сдвиге.
Аналогично для других элементарных трансляций 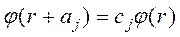 , где
, где 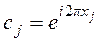 . Сдвиг на полный вектор решетки Браве
. Сдвиг на полный вектор решетки Браве 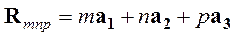 дает тогда
дает тогда 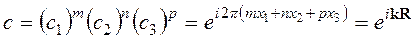 ,где
,где
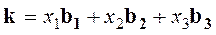
- волновой вектор в пространстве векторов обратной решетки b1,b2,b3.
Таким образом,
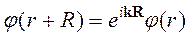 .
.
В принципе аналогичным путем можно доказать эту теорему и для вырожденных состояний уравнения Шредингера.
Другой путь доказательства этой теоремы основывается на известной теореме квантовой механики, что для коммутирующих операторов система волновых функций, описывающих их собственные состояния может быть выбрана одинаковой. Легко показать, что операторы гамильтониана и трансляций на вектор обратной решетки коммутируют. Тогда для коммутирующих операторов сдвига собственные числа являются чисто комплексными числами и находятся перемножением собственных чисел промежуточных трансляций:
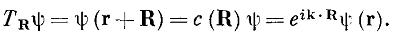
 2014-02-09
2014-02-09 3087
3087
