Следствия из теоремы Блоха
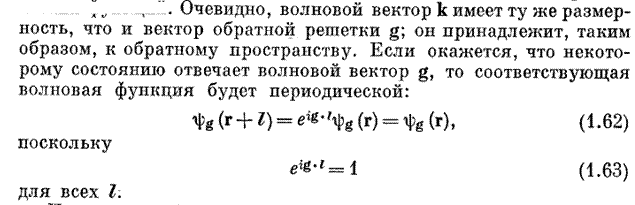
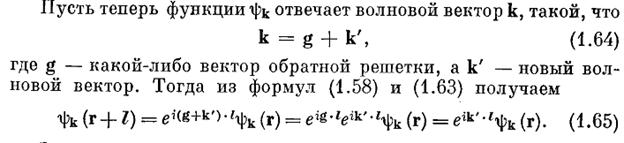

Пример одномерной решетки
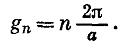
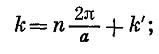
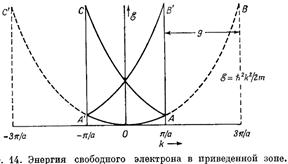
Приведенная зона Бриллюэна 
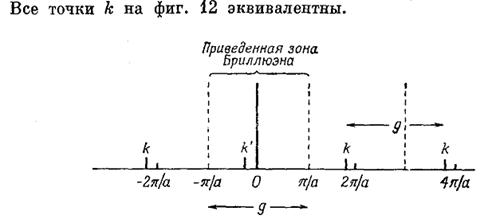
Двумерная решетка k’ = k - g
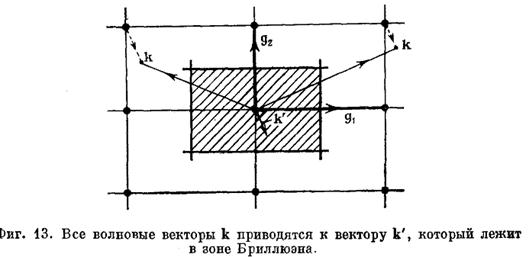
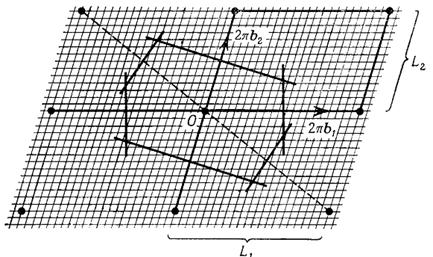
Пример разбиения двумерной зоны Бриллюэна косоугольной решетки Браве. В ячейке Вигнера-Зейтца обратной решетки содержится N=L1L2 «разрешенных» векторов kL.

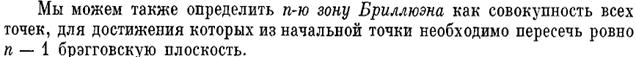
Рассмотрим одномерный кристалл ограниченных размеров L=Na. Если замкнуть решетку на себя, то должны выполняться циклические условия Борна-Кармана
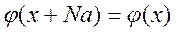 .
.
Согласно теореме Блоха 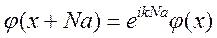 , поэтому должно быть
, поэтому должно быть 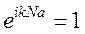 , откуда
, откуда 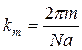 , где
, где 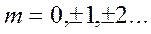
Для первой приведенной зоны Бриллюэна 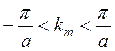
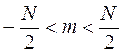 .
.
При четном N разрешенные значения попадают на края зоны Бриллюэна. При нечетном – не попадают.
В трехмерном случае элементарная ячейка не кубическая
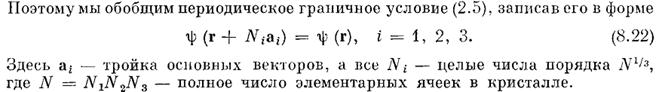
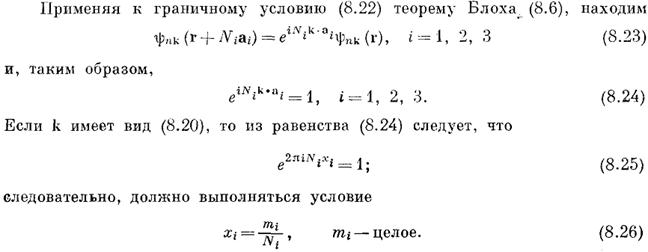
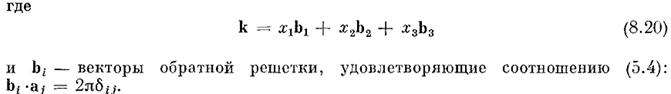
Отсюда следует, что объем 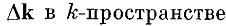 , приходящийся на одно разрешенное значение
, приходящийся на одно разрешенное значение 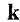 равен объему параллелепипеда с ребрами
равен объему параллелепипеда с ребрами 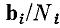
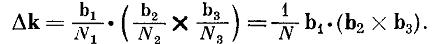
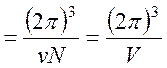
где N=N1N2N3 - число элементарных ячеек в кристалле.
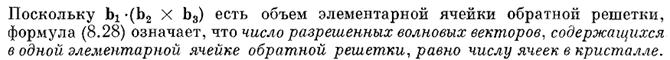
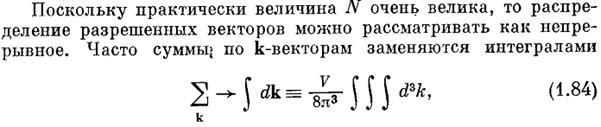
Свойства волнового числа и квазиимпульс.

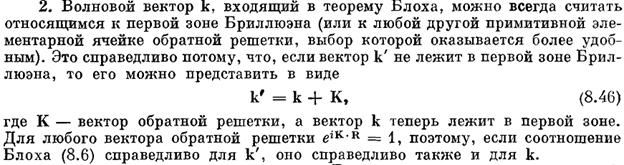

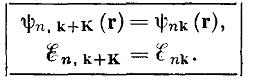

 2014-02-09
2014-02-09 2745
2745







