Используя формулу умножения комплексных чисел (3.3), получим формулу возведения комплексного числа в степень, называемую формулой Муавра.
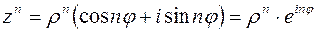 | (3.5) |
Из нее следует, что для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель этой степени.
Перейдем к процедуре извлечения корней. Известно, что в множестве действительных чисел не из всякого действительного числа можно извлечь корень. Например, 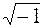 не существует. В множестве комплексных чисел дело обстоит иначе.
не существует. В множестве комплексных чисел дело обстоит иначе.
Пусть 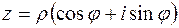 . Комплексное число
. Комплексное число 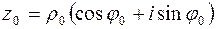 называется корнем
называется корнем 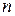 -й степени из
-й степени из 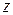 , если
, если 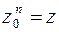 , т.е.
, т.е.
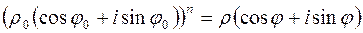
или
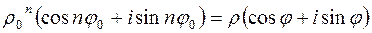 .
.
Модуль комплексного числа определяется однозначно, поэтому 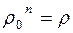 или
или 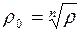 (здесь имеется в виду арифметический корень).
(здесь имеется в виду арифметический корень).
Аргумент комплексного числа определяется с точностью до 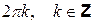 . Следовательно,
. Следовательно, 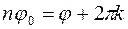 , а
, а 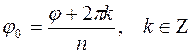 .
.
Таким образом, комплексное число 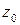 , которое является корнем
, которое является корнем 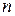 -й степени из
-й степени из 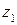 имеет вид:
имеет вид:
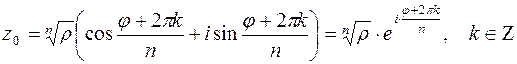 | (3.6) |
Придавая 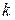 различные значения, мы не всегда будем получать различные корни. Действительно,
различные значения, мы не всегда будем получать различные корни. Действительно, 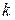 можно записать в виде
можно записать в виде 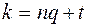 , где
, где 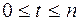 . Тогда
. Тогда 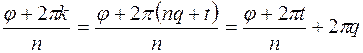 ,
,
Т.е. значение аргумента при данном 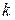 отличается от значения аргумента при
отличается от значения аргумента при 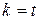 на число, кратное
на число, кратное 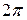 . Следовательно, в формуле (2) можно ограничится лишь значениями
. Следовательно, в формуле (2) можно ограничится лишь значениями 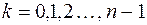 . При таких значениях
. При таких значениях 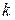 получаются различные корни, так как разность между их аргументами по абсолютной величине меньше
получаются различные корни, так как разность между их аргументами по абсолютной величине меньше 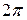 .
.
Итак, для каждого ненулевого числа 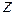 существует ровно
существует ровно  корней
корней  -й степени из
-й степени из 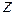 .
.
Пример. Вычислить 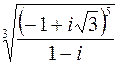 .
.
Представим число, стоящее под знаком корня в тригонометрической форме.
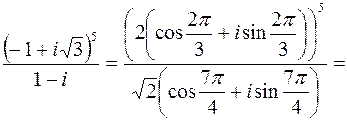
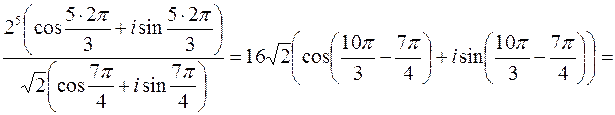
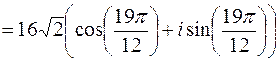 .
.
Извлечем далее корень третьей степени из этого комплексного числа
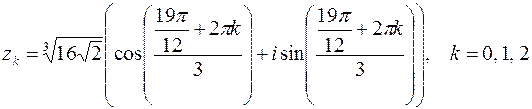 .
.
Отсюда полагая, что 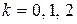 , получим
, получим
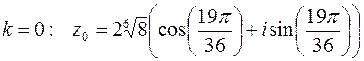 ;
;
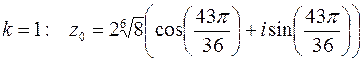 ;
;
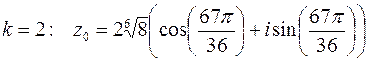 .
.
 2014-02-09
2014-02-09 6910
6910
